【题目】如图,二次函数![]() 的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
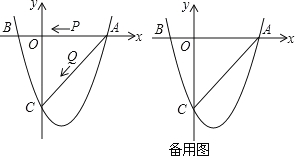
(1)求该二次函数的解析;
(2)若点P、Q同时从A点出发,以每秒1个单位长度的速度分别沿AB、AC边运动,其中一点到达端点时,另一点也随之停止运动.
①当点P运动到B点时,在x轴上是否存在点E,使得以A、E、Q为顶点的三角形为等腰三角形?若存在,请求出E点的坐标;若不存在,请说明理由.
②当P、Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请直接写出t的值及D点的坐标.
参考答案:
【答案】(1)![]() ;(2)①存在满足条件的点E,点E的坐标为
;(2)①存在满足条件的点E,点E的坐标为![]() 或
或![]() 或(﹣1,0)或(7,0);②
或(﹣1,0)或(7,0);②![]() ,
,![]()
【解析】
试题分析:(1)将A,B,C点坐标代入函数![]() 中,求得b、c,进而可求解析式;
中,求得b、c,进而可求解析式;
(2)等腰三角形有三种情况,AE=EQ,AQ=EQ,AE=AQ.借助垂直平分线,画圆易得E大致位置,设边长为x,表示其他边后利用勾股定理易得E坐标;
(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、D对称,则AP=DP,AQ=DQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等等性质可用t表示D点坐标,又D在E函数上,所以代入即可求t,进而D可表示.
试题解析:(1)∵二次函数![]() 的图象与x轴交于A(3,0),B(﹣1,0),C(0,﹣4).
的图象与x轴交于A(3,0),B(﹣1,0),C(0,﹣4).
∴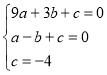 ,解得
,解得 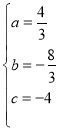 ,
,![]() ;
;
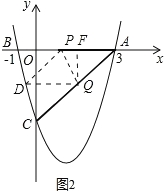
①存在.如图1,过点Q作![]() 于D,此时
于D,此时![]() ,∵A(3,0),B(﹣1,0),C(0,﹣4),O(0,0),
,∵A(3,0),B(﹣1,0),C(0,﹣4),O(0,0),![]()
![]() ∵当点P运动到B点时,点Q停止运动,
∵当点P运动到B点时,点Q停止运动,![]()
![]()
![]()
![]()
![]()
![]()
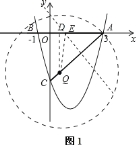
Ⅰ、作AQ的垂直平分线,交AO于E,此时AE=EQ,即△AEQ为等腰三角形,设![]() 则
则![]()
![]() 在
在![]() 中,
中,![]() 解得
解得![]()
![]()
![]() 说明点E在
说明点E在![]() 轴的负半轴上;Ⅱ、以Q为圆心,AQ长半径画圆,交
轴的负半轴上;Ⅱ、以Q为圆心,AQ长半径画圆,交![]() 轴于E,此时
轴于E,此时![]()
![]()
![]() 1.
1.![]()
![]() Ⅲ、当
Ⅲ、当![]() 时,2.当E在A点左边时,
时,2.当E在A点左边时,![]()
![]() 2.当E在A点右边时,
2.当E在A点右边时,![]()
![]() 综上所述,存在满足条件的点E,点E的坐标为
综上所述,存在满足条件的点E,点E的坐标为![]() 或
或![]() 或(﹣1,0)或(7,0).
或(﹣1,0)或(7,0).
②如图2,D点关于PQ与A点对称,过点Q作,![]() 于F,
于F,![]()
![]()
![]() ∴四边形AQDP为菱形,
∴四边形AQDP为菱形,![]()
![]()
![]()
![]()
![]()
![]()
![]() ∵D在二次函数
∵D在二次函数
![]() 上,
上,![]()
![]() 或
或![]() (与A重合,舍去),
(与A重合,舍去),![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):
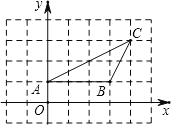
(1)点A关于原点对称的点的坐标为
(2)点C关于y轴对称的点的坐标为
(3)若△ABD与△ABC全等,则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:
(1)x2-4x
(2)﹣2x2﹢2
(3)4x5-4x4+x3
(4)

-
科目: 来源: 题型:
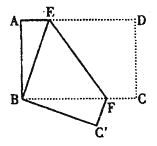
查看答案和解析>>【题目】如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C'处,折痕为EF,
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点M(-2,1)关于x轴对称点N的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四边形的边长依次为a、b、c、d,且a2+b2+c2+d2﹣2ac﹣2bd=0,则这个四边形的性状是
-
科目: 来源: 题型:
查看答案和解析>>【题目】用小数表示3.56×10﹣7为( )
A.0.000000356
B.0.0000000356
C.0.00000000356
D.0.000000000356
相关试题

