【题目】已知![]() 中弦
中弦![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )

A. AB=CD B. 弧AC=弧BD
C. PA=PD D. 弧AC=弧BC
参考答案:
【答案】D
【解析】
作OE⊥AB于E,OF⊥CD于F,如图,连结OA、OD,根据垂径定理得AE=BE,CF=DF,再根据角平分线定理得OE=OF,于是利用“HL”可证明Rt△AOE≌Rt△DOF,Rt△POE≌Rt△POF,得到AE=DF,PE=PF,易得AB=CD,PA=PD,则可对A选项和C选项进行判断;根据圆心角、弧、弦的关系有AB=CD得![]() ,易得
,易得![]() ,则可对B选项和D选项进行判断.
,则可对B选项和D选项进行判断.
作OE⊥AB于E,OF⊥CD于F,如图,连结OA、OD,
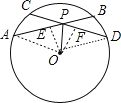
∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF,
∵PO平分∠APD,
∴OE=OF,
在Rt△AOE和Rt△DOF中,
![]() ,
,
∴Rt△AOE≌Rt△DOF,
∴AE=DF,
∴AB=CD,所以A选项的结论正确;
∴![]() ,
,
∴![]() ,即
,即![]() ,所以B选项的结论正确,D选项的结论错误;
,所以B选项的结论正确,D选项的结论错误;
在Rt△POE和Rt△POF中,
![]() ,
,
∴Rt△POE≌Rt△POF,
∴PE=PF,
∴AE+PE=DF+PF,
即PA=PD,所以C选项的结论错误.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt
 中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt
中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt , 过点D作DE⊥CB,垂足为点E.
, 过点D作DE⊥CB,垂足为点E.
(1) 依题意补全图形;
(2) 求证: AC=PE;
(3) 连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A表示一个数,若把数A写成形如
 的形式,其中
的形式,其中 、
、 、
、 、
、 、…都为整数.则我们称把数A写成连分数形式.
、…都为整数.则我们称把数A写成连分数形式.例如:把2.8写成连分数形式的过程如下:
2.8-2=0.8,
 ,
,1.25-1=0.25,
 ,
,4-4=0.

(1)把3.245写成连分数形式不完整的过程如下:
3.245-3=0.245,
 ,
,4.082-4=0.082,
 ,
,12.250-12=0.25,
 ,
,4-4=0.
∴

则
 _____________;
_____________; _____________;
_____________;(2)请把
 写成连分数形式;
写成连分数形式;(3)有这样一个问题:如图是长为47,宽为10的长方形纸片.从中裁剪出正方形,若长方形纸片无剩余,则剪出的正方形最少是几个?

小明认为这个问题和 “把一个数化为连分数形式” 有关联,并把
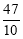 化成连分数从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数.
化成连分数从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,NE.下列结论:①AE=AF;②AM⊥EF;③△AEF是等边三角形;④DF=DN,⑤AD∥NE.其中正确的结论有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:如图1,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
(2)如图2所示,△ABC的顶点分别为A(﹣4,5),B(﹣3,2),C(4,﹣1)
①作出△ABC关于x轴对称的图形△A1B1C1;
②用三角板作出△ABC的AB边上的高CH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)若AB∥x轴,如图1,求t的值;
(2)设点A关于x轴的对称点为A′,连接A′B,在点P运动的过程中,∠OA′B的度数是否会发生变化,若不变,请求出∠OA′B的度数,若改变,请说明理由.
(3)如图2,当t=3时,坐标平面内有一点M(不与A重合)使得以M、P、B为顶点的三角形和△ABP全等,请直接写出点M的坐标.
相关试题

