Question

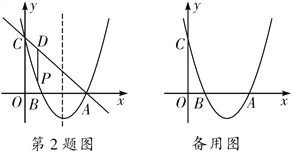
【题目】如图，抛物线y＝x2＋bx＋c过点A(3，0)，B(1，0)，交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动(点P不与点A重合)，过点P作PD∥y轴交直线AC于点D.

(1)求抛物线的解析式；

(2)求点P在运动的过程中线段PD长度的最大值；

(3)在抛物线对称轴上是否存在点M，使|MA－MC|最大？若存在，请求出点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线的解析式为y＝x2－4x＋3.（2）当x＝时，线段PD的长度有最大值.（3）存在点M(2，－3)，使|MA－MC|最大.

【解析】试题分析：（1）把点A、B的坐标代入抛物线解析式，解方程组得到b、c的值，即可得解；

（2）求出点C的坐标，再利用待定系数法求出直线AC的解析式，再根据抛物线解析式设出点P的坐标，然后表示出PD的长度，再根据二次函数的最值问题解答；

（3）根据抛物线的对称性可知MA=MB，再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时，|MA﹣MC|最大，然后利用待定系数法求出直线BC的解析式，再求解即可．

试题解析：（1）∵抛物线y=x2+bx+c过点A（3，0），B（1，0），

∴，

解得，

∴抛物线解析式为y=x2﹣4x+3；

（2）令x=0，则y=3，

∴点C（0，3），

则直线AC的解析式为y=﹣x+3，

设点P（x，x2﹣4x+3），

∵PD∥y轴，

∴点D（x，﹣x+3），

∴PD=（﹣x+3）﹣（x2﹣4x+3）=﹣x2+3x=﹣（x﹣）2+，

∵a=﹣1＜0，

∴当x=时，线段PD的长度有最大值；

（3）由抛物线的对称性，对称轴垂直平分AB，

∴MA=MB，由三角形的三边关系，|MA﹣MC|＜BC，

∴当M、B、C三点共线时，|MA﹣MC|最大，为BC的长度，

设直线BC的解析式为y=kx+b（k≠0），

则，

解得，

∴直线BC的解析式为y=﹣3x+3，

∵抛物线y=x2﹣4x+3的对称轴为直线x=2，

∴当x=2时，y=﹣3×2+3=﹣3，

∴点M（2，﹣3），

即，抛物线对称轴上存在点M（2，﹣3），使|MA﹣MC|最大．