搜索
【题目】如图，已知反比例函数
的图象经过点
，过点A作
轴于点B，连结
．
（1）求k的值；
（2）如图，若直线
经过点A，与x轴相交于点C，且满足
．求：
①直线的表达式；
②记直线与双曲线的另一交点为
，试求
的面积
．
参考答案：
【答案】（1）
；（2）①直线
的表达式为
，②
．
【解析】
（1）由点A的坐标利用反比例函数图象上点的坐标特征即可求出k值；
（2）①根据
可得出OB=OC，再由点A的坐标即可得出点B、C的坐标，结合点A、C的坐标利用待定系数法即可求出直线AC的表达式；
②根据点D的纵坐标即可求出点D的坐标，结合三角形的面积公式可求出△AOD的面积．
（1）∵反比例函数
的图象经过点
，
∴
．
（2）①∵，
∴
，
∴
．
∵点，
∴点
，点
．
将点、代入
中，
得：
，解得：
，
∴直线的表达式为．
②连接
，如图所示．
∵点
，
∴
．
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩（分）
7
6
8
7
7
5
8
7
8
7
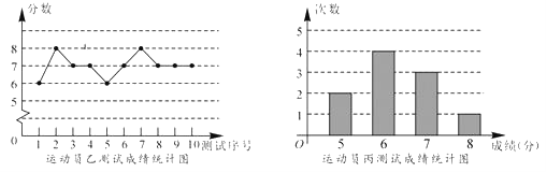
（1）写出运动员甲测试成绩的众数和中位数；
（2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适?为什么?(参考数据：三人成绩的方差分别为
、
、
) -
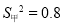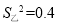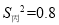科目： 来源： 题型：
查看答案和解析>>【题目】如图，放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在Y轴上，点B1、B2、B3…都在直线
上，则点A2016的坐标为（ ）
A. （2016
，2018） B. （2016，2016） C. （2016，2016） D. （2016，2018） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知O为直线AB上的一点，射线OA表示正北方向，∠COE＝90°，射线OF平分∠AOE．
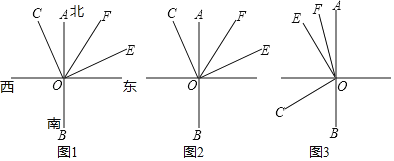
（1）如图1，若∠AOE＝70°，则∠COF的度数是 ；
（2）若将∠COE绕点O旋转至图2的位置，试判断∠COF和∠BOE之间的数量关系，并证明你的证明；
（3）若将∠COE绕点O旋转至图3的位置，直接写出2∠COF+∠BOE的度数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O，D是弧BC的中点，OD交BC于点H，且OH=DH，连接AD，过点B作BE⊥AD于点E，连接EH，BF⊥AC于M，若AC=5，EH=
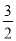，则AF=_____．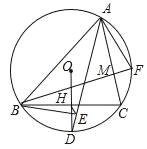
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在△ABC中，∠ACB=90°，AC=BC，∠PCQ=45°，把∠PCQ绕点C旋转，在整个旋转过程中，过点A作AD⊥CP，垂足为D，直线AD交CQ于E．
（1）如图①，当∠PCQ在∠ACB内部时，求证：AD+BE=DE；
（2）如图②，当CQ在∠ACB外部时，则线段AD、BE与DE的关系为_____；
（3）在（1）的条件下，若CD=6，S△BCE=2S△ACD，求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在同一直线上的三点A，B，C，若满足点C到另两个点A，B的距离之比是2，则称点C是其余两点的亮点（或暗点）．具体地，当点C在线段AB上时，若
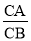＝2，则称点C是[A，B]的亮点；若
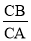＝2，则称点C是[B，A]的亮点；当C在线段AB的延长线上时，若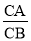＝2，称点C是[A，B]的暗点．例如，如图1，数轴上点A，B，C，D分别表示数﹣1，2，1，0．则点C是[A，B]的亮点，又是[A，D]的暗点；点D是[B，A]的亮点，又是[B，C]的暗点
（1）如图2，M，N为数轴上两点，点M所表示的数为﹣2，点N所表示的数为4．
[M，N]的亮点表示的数是 ，[N，M]的亮点表示的数是 ；
[M，N]的暗点表示的数是 ，[N，M]的暗点表示的数是 ；
（2）如图3，数轴上点A所表示的数为﹣20，点B所表示的数为40．一只电子蚂蚁P从B出发以2个单位每秒的速度向左运动，设运动时间为t秒．
①求当t为何值时，P是[B，A]的暗点；
②求当t为何值时，P，A和B三个点中恰有一个点为其余两点的亮点．
相关试题
