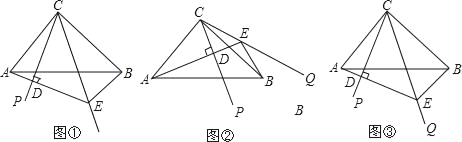
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.
参考答案:
【答案】(1)见解析 (2)AD=BE+DE (3)8
【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;
(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;
(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.
试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
故答案为:AD=BE+DE.
(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,∴△ECF是等腰直角三角形,∴CD=DF=DE=6.∵S△BCE=2S△ACD,∴AF=2AD,∴AD=![]() ×6=2,∴AE=AD+DE=2+6=8.
×6=2,∴AE=AD+DE=2+6=8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上的一点,射线OA表示正北方向,∠COE=90°,射线OF平分∠AOE.
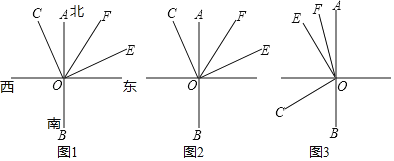
(1)如图1,若∠AOE=70°,则∠COF的度数是 ;
(2)若将∠COE绕点O旋转至图2的位置,试判断∠COF和∠BOE之间的数量关系,并证明你的证明;
(3)若将∠COE绕点O旋转至图3的位置,直接写出2∠COF+∠BOE的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
 的图象经过点
的图象经过点 ,过点A作
,过点A作 轴于点B,连结
轴于点B,连结 .
.(1)求k的值;
(2)如图,若直线
 经过点A,与x轴相交于点C,且满足
经过点A,与x轴相交于点C,且满足 .求:
.求:①直线
 的表达式;
的表达式;②记直线
 与双曲线
与双曲线 的另一交点为
的另一交点为 ,试求
,试求 的面积
的面积 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,D是弧BC的中点,OD交BC于点H,且OH=DH,连接AD,过点B作BE⊥AD于点E,连接EH,BF⊥AC于M,若AC=5,EH=
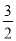 ,则AF=_____.
,则AF=_____.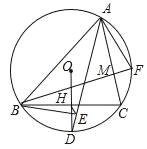
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直线上的三点A,B,C,若满足点C到另两个点A,B的距离之比是2,则称点C是其余两点的亮点(或暗点).具体地,当点C在线段AB上时,若
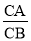 =2,则称点C是[A,B]的亮点;若
=2,则称点C是[A,B]的亮点;若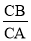 =2,则称点C是[B,A]的亮点;当C在线段AB的延长线上时,若
=2,则称点C是[B,A]的亮点;当C在线段AB的延长线上时,若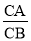 =2,称点C是[A,B]的暗点.例如,如图1,数轴上点A,B,C,D分别表示数﹣1,2,1,0.则点C是[A,B]的亮点,又是[A,D]的暗点;点D是[B,A]的亮点,又是[B,C]的暗点
=2,称点C是[A,B]的暗点.例如,如图1,数轴上点A,B,C,D分别表示数﹣1,2,1,0.则点C是[A,B]的亮点,又是[A,D]的暗点;点D是[B,A]的亮点,又是[B,C]的暗点
(1)如图2,M,N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
[M,N]的亮点表示的数是 ,[N,M]的亮点表示的数是 ;
[M,N]的暗点表示的数是 ,[N,M]的暗点表示的数是 ;
(2)如图3,数轴上点A所表示的数为﹣20,点B所表示的数为40.一只电子蚂蚁P从B出发以2个单位每秒的速度向左运动,设运动时间为t秒.
①求当t为何值时,P是[B,A]的暗点;
②求当t为何值时,P,A和B三个点中恰有一个点为其余两点的亮点.
-
科目: 来源: 题型:
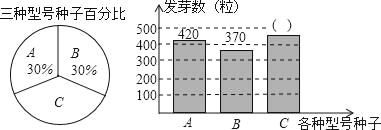
查看答案和解析>>【题目】松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图:
(1)求C型号种子的发芽数;
(2)通过计算说明,应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中E是BC边上一点,且AB=AE,AE,DC的延长线相交于点F.

(1)若∠F=62°,求∠D的度数;
(2)若BE=3EC,且△EFC的面积为1,求平行四边形ABCD的面积.
相关试题

