【题目】为建设京西绿色走廊,改善永定河水质,某治污公司决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格与月处理污水量如下表:

经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求x、y的值;
(2)如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;
(3)在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.
参考答案:
【答案】(1)![]() ;
;
(2)该公司有以下三种方案:A型设备0台,B型设备为10台;A型设备1台,B型设备为9台;A型设备2台,B型设备为8台
(3)购买A型设备1台,B型设备9台最省钱.
【解析】试题分析:(1)购买A型的价格是x万元,购买B型的设备y万元,根据购买一台A型号设备比购买一台B型号设备多2万元,购买2台A型设备比购买3台B型号设备少6万元,可列方程组求解.(2)设购买A型号设备a台,则B型为(10-a)台,根据使治污公司购买污水处理设备的资金不超过105万元,进而得出不等式;(3)利用每月要求处理污水量不低于2040吨,可列不等式求解.
试题解析:(1)由题意,得 ![]()
解得![]()
(2)设治污公司决定购买A型设备a台,则购买B型设备(10-a)台.
由题意,得 ![]()
解得 ![]()
所以,该公司有以下三种方案:
A型设备0台,B型设备为10台;
A型设备1台,B型设备为9台;
A型设备2台,B型设备为8台
(3)由题意,得 ![]()
解得: ![]()
所以,购买A型设备1台,B型设备9台最省钱
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x﹣4)2=2x﹣3化为一般式是( )
A. x2﹣10x+13=0 B. x2﹣10x+19=0 C. x2﹣6x+13=0 D. x2﹣6x+19=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
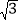 ≈1.73).
≈1.73).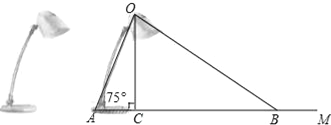
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”。
(1)请问一元二次方程x2-3x+2=0是倍根方程吗?如果是,请说明理由。
(2)若一元二次方程ax2+bx-6=0是倍根方程,且方程有一个根为2,求a、b的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年初,某服装经销商发现某款新型运动服市场需求量较大,该服装的进价为200元/件,每年支付员工工资和场地租金等其它费用总计40000元.经过市场调查发现若销售单价为x元/件,则年销售量为(800-x)件.
(1)用含x的代数式表示年获利金额w;
(注:年获利=(销售单价-进价)×年销售量-其它费用)
(2)若经销商希望该服装一年的销售获利达40000元,且要使产品销售量较大,你认为销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
 BD;其中正确结论的是( )
BD;其中正确结论的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是_____.
相关试题

