【题目】如图在Rt△ABC=90![]() ,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
,如果CD、CM分别是斜边上的高和中线,AC=2,BC=4,那么下列结论中错误的是( )
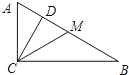
A. ∠ACD=∠BB. CM=![]() C. ∠B=30
C. ∠B=30![]() D. CD=
D. CD=![]()
参考答案:
【答案】C
【解析】
根据同角的余角相等判断A;根据勾股定理和直角三角形的性质判断B;根据三角形的面积公式计算,判断D.
∵∠ACB=90°,∴∠ACD+∠BCD=90°.
∵CD⊥AB,∴∠B+∠BCD=90°,∴∠ACD=∠B,故A正确,不符合题意;
在Rt△ACB中,AB![]() 2
2![]() .
.
∵∠ACB=90°,CM是斜边上的中线,∴CM![]() ,故B正确,不符合题意;
,故B正确,不符合题意;
在Rt△ACB中,AB=2![]() ,AC=2,∴∠B≠30°,故C错误,符合题意;
,AC=2,∴∠B≠30°,故C错误,符合题意;
![]() 2×4
2×4![]() 2
2![]() CD,解得:CD
CD,解得:CD![]() ,故D正确,不符合题意.
,故D正确,不符合题意.
故选C.
-
科目: 来源: 题型:
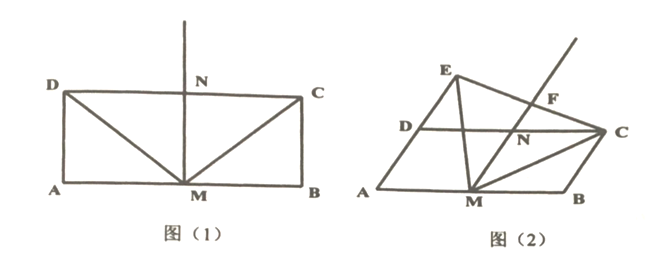
查看答案和解析>>【题目】如图(1),在矩形
 中,
中, 分别是
分别是 的中点,作射线
的中点,作射线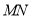 ,连接
,连接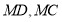 .
.
(1)请直接写出线段
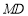 与
与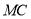 的数量关系;
的数量关系;(2)将矩形
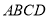 变为平行四边形,其中
变为平行四边形,其中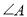 为锐角,如图(2),
为锐角,如图(2),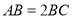 ,
,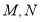 分别是
分别是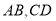 的中点,过点
的中点,过点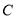 作
作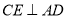 交射线
交射线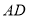 于点
于点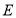 ,交射线
,交射线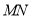 于点
于点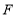 ,连接
,连接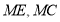 ,求证:
,求证: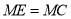 ;
;(3)写出
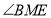 与
与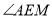 的数量关系,并证明你的结论.
的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=13,BC=14,AC=15,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,则AE+CF的最大值为_____,最小值为_____.
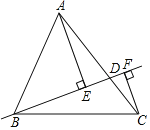
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,两条直角边长分别为a,b,斜边长为c.如图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)若Rt△ABC的两直角边之比均为2:3.现随机向该图形内掷一枚小针,则针尖落在四个直角三角形区域的概率是多少?
(2)若正方形EFMN的边长为8,Rt△ABC的周长为18,求Rt△ABC的面积.
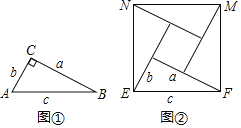
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
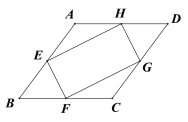
A. AB=
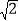 EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=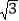 EF D. AB=
EF D. AB=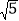 EF
EF -
科目: 来源: 题型:
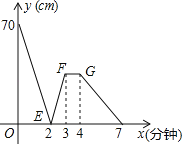
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 m,甲机器人前2min的速度为 m/min.
(2)若前3min甲机器人的速度不变,求出前3min,甲、乙两机器人之间的距离y(m)与他们的行走时间r(min)之间的关系式.
(3)求出两机器人出发多长时间相距28m.
相关试题

