【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
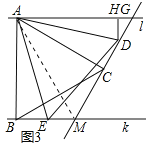
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.

参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)当2<DH<4时,BC∥DE.理由见解析.
;(2)证明见解析;(3)当2<DH<4时,BC∥DE.理由见解析.
【解析】(1)证明△ABE≌△BCF,即可求得AE的长,然后利用勾股定理即可求解;
(2)过B作BE⊥l于点E,交k于点F,易证△AEB∽△BCF,然后分AB是长和AB是宽两种情况进行讨论求得;
(3)连接AC,证明直角△AEC≌直角△AFD即可证得;
(4)首先证明AM⊥BC,然后证明Rt△ABE≌Rt△ACD,得到∠BAE=∠CAD,则AM⊥ED,即可证得BC∥DE.
(1)解:∵l∥k,BE⊥l,
∴∠BFC=∠BEA=90°,
∴∠ABE+∠BAE=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∴∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,∠BEA=∠CFB,∠BAE=∠CBF,AB=BC
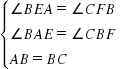
,∴△ABE≌△BCF(AAS),
∴AE=BF,
∵d1=d3=1,d2=2,
∴BE=3,AE=1,
在直角△ABE中,AB=![]() =
=![]() =
=![]() ,
,
即正方形的边长是![]() ;
;
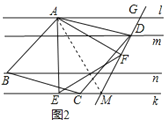
(2)证明:连接AC,如图2所示:
∵四边形ABCD是菱形,且∠ADC=60°,
∴AC=AD,
∵△AEF是等边三角形,
∴AE=AF,
∵AE⊥k,∠AFD=90°,
∴∠AEC=∠AFD=90°,
在Rt△AEC和Rt△AFD中,AC=AD,AE=AF,
![]() ,
,
∴Rt△AEC≌Rt△AFD(HL),
∴EC=DF;
(3)解:当2<DH<4时,BC∥DE.理由如下:
如图3所示,当2<DH<4时,点D在线段CM上,连接AM,
则∠ABM=∠ACM=90°,AB=AC,AM=AM,
在Rt△ABM和Rt△ACM中,AM=AM,AB=AC,
![]() ,
,
∴Rt△ABM≌Rt△ACM(HL),
∴∠BAM=∠CAM,
∴AM⊥BC,
在Rt△ABE和Rt△ACD中,AE=AD,AB=AC,
![]() ,
,
∴Rt△ABE≌Rt△ACD(HL),
∴∠BAE=∠CAD,
∴∠EAM=∠DAM,
∴AM⊥ED,
∴BC∥DE.
“点睛”本题考查了全等三角形的判定与性质以及相似三角形的判定与性质,正确构造相似的三角形是关键,解题时根据题意正确作出辅助线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
项目品牌
单价/元
购买数量/台
购买费用/元
A
800
x
B
1000
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣2+(
)﹣2+( 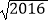 ﹣
﹣ 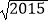 )0+|
)0+| 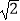 ﹣1|+(
﹣1|+( 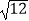 ﹣3
﹣3 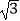 )tan60°.
)tan60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.

(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M,N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.求证:∠BQM=60°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台举办的“2016年春节联欢晚会”受到广泛关注,某民间组织就2016年春节联欢晚会节目的喜爱程度,在丽州广场进行了问卷调查,并将问卷调查结果分为“非常喜欢”“比较喜欢”“感觉一般”“不太喜欢”四个等级,分别记作A,B,C,D,根据调查结果绘制出如图所示的“扇形统计图”和“条形统计图”,请结合图中所给信息解答下列问题:
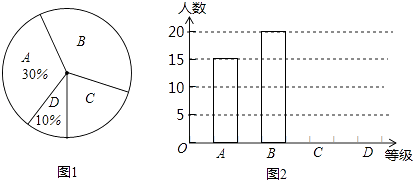
(1)这次被调查对象共有人,被调查者“不太喜欢”有人;
(2)补全扇形统计图和条形统计图;
(3)在“非常喜欢”调查结果里有5人为80后,分别为3男2女,在这5人中,该民间组织打算随机抽取2人进行采访,请你用列表法或列举法求出所选2人均为男生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】节能电动车越来越受到人们的喜欢,新开发的各种品牌电动车相继投入市场.小李车行经营的A型节能电动车2015年销售总额为m万元,2016年每辆A型节能电动车的销售价比2015年降低2000年,若2015年和2016年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则2016年的销售总额比2015年减少20%.
(1)2016年A型节能电动车每辆售价多少万元?(用列方程方法解答)
(2)小李车行计划端午节后新购进一批A型节能电动车和新型B型节能电动车,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且2016年A,B两种型号节能电动车的进货和销售价格如表,那么2016年新款B型节能电动车至少要购进多少辆?A型节能电动车
B型节能电动车
进货价格(万元/辆)
0.55
0.7
销售价格(万元/辆)
2016年的销售价格
2
相关试题

