【题目】如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线l的对称的△A1B1C1.
(2)画出△ABC关于点P的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形_______________(是或否)轴对称图形,如果是轴对称图形,请画出对称轴.

参考答案:
【答案】(1)见解析;(2)见解析;(3)是,见解析
【解析】试题分析:(1)根据△ABC与△A1B1C1关于直线OM对称进行作图即可;
(2)根据△ABC与△A2B2C2关于点O成中心对称进行作图即可;
(3)一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴.
试题解析:
(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)如图,△A1B1C1与△A2B2C2组成的图形是轴对称图形,其对称轴为直线l.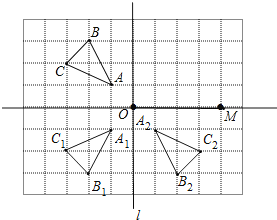
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=
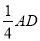 ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙D的直径,AD切⊙D于点A,EC=CB.则下列结论:①BA⊥DA; ②OC∥AE;③∠COE=2∠CAE;④OD⊥AC.一定正确的个数有( )

A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

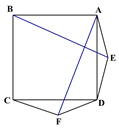

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为 (一1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c>0;④当y>0时,x的取值范围是﹣1≤x<3;⑤若(﹣ ,y1),(
,y1),(  ,y2)是抛物线上两点,则y1<y2 .
,y2)是抛物线上两点,则y1<y2 .
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在1×3的正方形网格格点上放三枚棋子,按图所示的位置己放置了两枚棋子,若第三枚棋子随机放在其他格点上,则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为 .
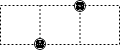
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
相关试题

