【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想: ①若∠A=20°,∠D=40°,求∠AED的度数
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用: 如图②,射线FE与l1 , l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).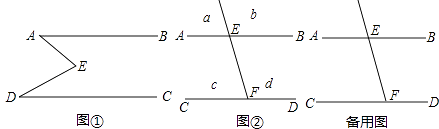
参考答案:
【答案】
(1)解:①过E作EF∥AB,
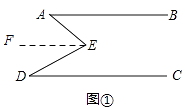
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF=20°,∠D=∠DEF=40°,
∴∠AED=∠AEF+∠DEF=∠A+∠D=60°,
②∠AED=∠A+∠D,
证明:方法一、延长DE交AB于F,如图1,
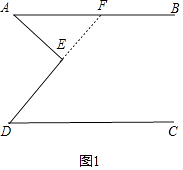
∵AB∥CD,
∴∠DFA=∠D,
∴∠AED=∠A+∠DFA;
方法二、过E作EF∥AB,如图2,
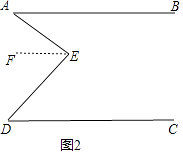
∵AB∥CD,
∴AB∥EF∥CD,
∴∠A=∠AEF,∠D=∠DEF,
∴∠AED=∠AEF+∠DEF=∠A+∠D
(2)解:当P在a区域时,如图3,∠PEB=∠PFC+∠EPF;
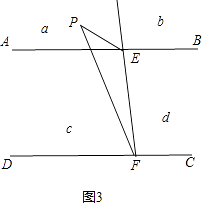
当P点在b区域时,如图4,∠PFC=∠PEB+∠EPF;
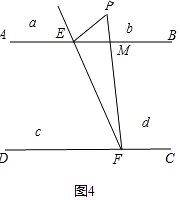
当P点在区域c时,如图5,∠EPF+∠PEB+∠PFC=360°;
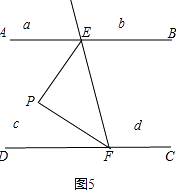
当P点在区域d时,如图6,∠EPF=∠PEB+∠PFC.
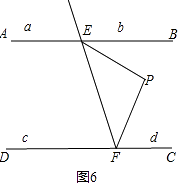
【解析】(1)①过E作EF∥AB,根据AB∥CD,可得AB∥EF∥CD,再根据两直线平行,内错角相等进行计算即可;②作辅助线构造内错角,依据两直线平行,内错角相等或三角形外角性质,进行计算即可;(2)根据a,b,c,d分别是被射线FE隔开的4个区域,P是位于四个区域上的点,画出对应的图形,进而得出结论.
【考点精析】本题主要考查了平行线的性质和三角形的外角的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m,n分别为一元二次方程x2-2x-2018=0的两个实数根,则m2-m+n=_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值
②求:24m﹣6n的值
(2)已知2×8x×16=223 , 求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)
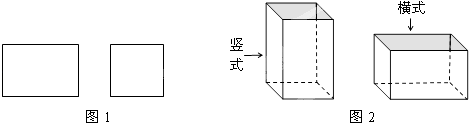
(1)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线b、c被直线a所截,则∠1与∠2是( )
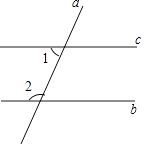
A.同位角
B.同旁内角
C.内错角
D.对顶角 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:

(1)△ACE≌△BCD;
(2)AD2+DB2=DE2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E,F.
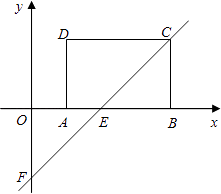
(1)求矩形ABCD的顶点A,B,C,D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x﹣2上一点,若S△POE=5,求点P的坐标.
相关试题

