【题目】综合题
(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值
②求:24m﹣6n的值
(2)已知2×8x×16=223 , 求x的值.
参考答案:
【答案】
(1)解:∵4m=a,8n=b,
∴22m=a,23n=b,
22m+3n=22m23n=ab;
②24m﹣6n=24m÷26n=(22m)2÷(23n)2= ![]()
(2)解∵2×8x×16=223,
∴2×(23)x×24=223,
∴2×23x×24=223,
∴1+3x+4=23,
解得:x=6:
【解析】(1)分别将4m , 8n化为底数为2的形式,然后代入①②求解;(2)将8x化为23x , 将16化为24 , 列出方程求出x的值.
【考点精析】本题主要考查了同底数幂的除法的相关知识点,需要掌握同底数幂的除法法则:am÷an=am-n(a≠0,m,n都是正整数,且m>n)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】万安县开发区某电子电路板厂到井冈山大学从2014年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5:3:2的比例记入每人的最后总分,有4位应聘者的得分如表.
得分
应聘人
项目专业知识
英语水平
参加社会实践与
社团活动等甲
85
85
90
乙
85
85
70
丙
80
90
70
丁
90
90
50
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+4x-2=0,那么3x2+12x+2002的值为 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m,n分别为一元二次方程x2-2x-2018=0的两个实数根,则m2-m+n=_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)
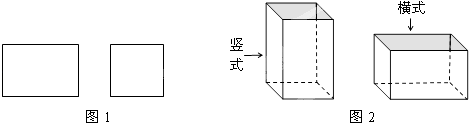
(1)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想: ①若∠A=20°,∠D=40°,求∠AED的度数
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用: 如图②,射线FE与l1 , l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).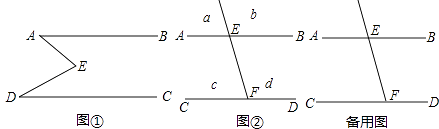
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线b、c被直线a所截,则∠1与∠2是( )
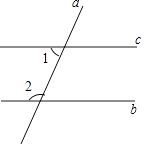
A.同位角
B.同旁内角
C.内错角
D.对顶角
相关试题

