搜索
【题目】如图，在△ABC中，AC=2，∠BA C=75°，∠ACB= 60°，高BE与AD相交于点H,则DH的长为
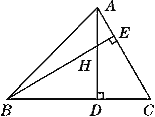
A. 2 B. 1.5 C. 1 D. 0.5
参考答案：
【答案】C
【解析】
根据∠BAC=75°，∠C=60°，得出∠BAD=45°，利用等腰直角三角形的性质和全等三角形的判定和性质得出DH=DC，再利用30°角所对直角边等于斜边的一半即可得到结论．
∵∠BAC=75°，且高BE与AE相交于H，∠C=60°，∴∠DAC=∠EBD=30°，∴∠BAD=45°，∴△BAD是等腰直角三角形，∴BD=AD．
在△BDH与△ADC中，∵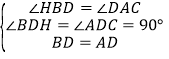
，∴△BDH≌△ADC（AAS），∴DH=DC．∵∠DAC=30°，∴CD=
AC=1，∴DH=1.
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1． ①b2＞4ac；②b＜0；③y随x的增大而减小；④若（﹣2，y1），（5，y2）是抛物线上的两点，则y1＜y2 ， 上述4个判断中，正确的是（ ）
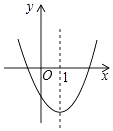
A.①②④
B.①④
C.①③④
D.②③④ -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面语句：
① 一个数的k 次方（k是整数）的立方根是正数．
②如果一个数的立方根等于它本身，那么这个数或者是1，或者是0．
③如果a≠0，那么a的立方根的符号与a的符号相同．
④一个正数的算术平方根以及它的立方根都小于原来的数．
⑤两个互为相反数的数开立方所得的结果仍然互为相反数．
在上面语句中，正确的有（ ）
A. 1句 B. 2句 C. 3句 D. 4句
-
科目： 来源： 题型：
查看答案和解析>>【题目】求下列各式中x的值.
(1) (x-1)3=27;
(2)x3+1=-
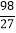;(3)
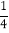(2x+3)3=54;(4) 27(2x-1)3+2=66.
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列式子,并解决问题.
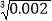≈0.1260;
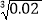≈0.2714;
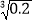≈0.5848;
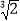≈1.260;
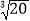≈2.714.(1)
≈ ,
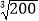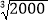≈ ;(2)若
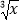≈58.48,则x≈ ;(3)通过类比,你能得到什么规律?用一句话描述出来.
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数
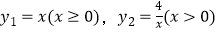的图象如图所示，则结论： ①两函数图象的交点A的坐标为（2，2）；
②当x＞2时，y2＞y1；
③当x=1时，BC=3；
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是 ．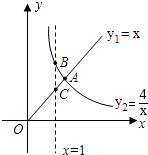
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点．若AE＝2，当EF＋CF取得最小值时，∠ECF的度数为( )
A. 20° B. 25° C. 30° D. 45°
相关试题
