【题目】请阅读材料并填空:
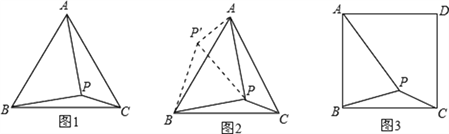
如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1.求∠BPC的度数和等边三角形ABC的边长.
,PC=1.求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:
将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2).连接PP′.
(1)根据李明同学的思路,进一步思考后可求得∠BPC= °,等边△ABC的边长为 .
(2)请你参考李明同学的思路,探究并解决下列问题:
如图3,在正方形ABCD内有一点P,且PA= ![]() ,BP=
,BP= ![]() ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.
参考答案:
【答案】(1)150, ![]() ;(2) ∠BPC=135°, 正方形边长为
;(2) ∠BPC=135°, 正方形边长为![]() .
.
【解析】(1)∠BPC=150°, ………………2分
等边△ABC的边长为![]() . ………………4分
. ………………4分
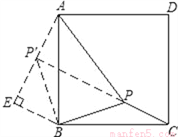
( 2) 如图,
将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.
∴AP′=PC=1,BP=BP′=![]() ;
;
连接PP′,
在Rt△BP′P中,
∵BP=BP′=![]() ,∠PBP′=90°,
,∠PBP′=90°,
 ∴PP′=2,∠BP′P=45°; ………………6分
∴PP′=2,∠BP′P=45°; ………………6分
在△AP′P中,AP′=1,PP′=2,AP=![]() ,
,
∵![]() ,即AP′2+PP′2=AP2;
,即AP′2+PP′2=AP2;
∴△AP′P是直角三角形,即∠AP′P=90°,
∴∠AP′B=135°,
∴∠BPC=∠AP′B=135°. ………………8分
过点B作BE⊥AP′,交AP′的延长线于点E;则△BEP′是等腰直角三角形,
∴∠EP′B=45°,
∴EP′=BE=1,
∴AE=2;
∴在Rt△ABE中,由勾股定理,得AB=![]() ; ………………10分
; ………………10分
∴∠BPC=135°,正方形边长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为( )
A. 5 B. ﹣1 C. 2 D. ﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一个正数的两个平方根分别是2a﹣2和a﹣4,则a的值是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写一个随机事件:___________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=Rt∠,直角边AB、BC的长(AB<BC)是方程
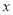 2-7
2-7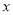 +12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).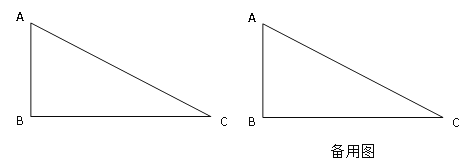
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为
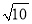 时运动时间t的值;
时运动时间t的值;(3)点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
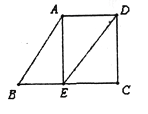
查看答案和解析>>【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
相关试题

