【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
参考答案:
【答案】
(1)
解:令y=0,解得x1=﹣1或x2=3
∴A(﹣1,0)B(3,0)
将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3
∴C(2,﹣3)
∴直线AC的函数解析式是y=﹣x﹣1
(2)
解:设P点的横坐标为x(﹣1≤x≤2)
则P、E的坐标分别为:P(x,﹣x﹣1)
E(x,x2﹣2x﹣3)
∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当 ![]() 时,PE的最大值=
时,PE的最大值= ![]()
(3)
解:存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+ ![]() ,0),F4(4﹣
,0),F4(4﹣ ![]() ,0).
,0).
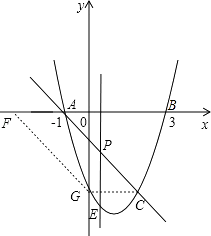
①如图,连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);

②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);

③如图,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+ ![]() ,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+
,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+4+ ![]() .因此直线GF与x轴的交点F的坐标为(4+
.因此直线GF与x轴的交点F的坐标为(4+ ![]() ,0);
,0);

④如图,同③可求出F的坐标为(4﹣ ![]() ,0).
,0).
综合四种情况可得出,存在4个符合条件的F点
【解析】(1)因为抛物线与x轴相交,所以可令y=0,解出A、B的坐标.再根据C点在抛物线上,C点的横坐标为2,代入抛物线中即可得出C点的坐标.再根据两点式方程即可解出AC的函数表达式;(2)根据P点在AC上可设出P点的坐标.E点坐标可根据已知的抛物线求得.因为PE都在垂直于x轴的直线上,所以两点之间的距离为yp﹣yE , 列出方程后结合二次函数的性质即可得出答案;(3)存在四个这样的点.①连接C与抛物线和y轴的交点,那么CG∥x轴,此时AF=CG=2,因此F点的坐标是(﹣3,0);②AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);③此时C,G两点的纵坐标关于x轴对称,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1+ ![]() ,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+7.因此直线GF与x轴的交点F的坐标为(4+
,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将G点代入后可得出直线的解析式为y=﹣x+7.因此直线GF与x轴的交点F的坐标为(4+ ![]() ,0);④如图,同③可求出F的坐标为(4﹣
,0);④如图,同③可求出F的坐标为(4﹣ ![]() ,0);
,0);
综合四种情况可得出,存在4个符合条件的F点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(﹣1,0)、B(3,0).

(1)求抛物线的解析式;
(2)在直线BC上方的抛物线上找一点P,使△PBC的面积最大,求P点的坐标;
(3)如图2,连接BD、CD,抛物线的对称轴与x轴交于点E,过抛物线上一点M作MN⊥CD,交直线CD于点N,求当∠CMN=∠BDE时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用下面的方法求出方程2
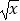 ﹣3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
﹣3=0的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.方程
换元法得新方程
解新方程
检验
求原方程的解
2
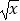 ﹣3=0
﹣3=0令
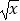 =t,则2t﹣3=0
=t,则2t﹣3=0t=

t=
 >0
>0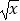 =
=  ,所以x=
,所以x= 
x﹣2
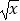 +1=0
+1=0x+2+
 =0
=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决后面的问题. 材料:我们知道,n个相同的因数a相乘
 可记为an , 如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b (a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4)
可记为an , 如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b (a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4)
(1)计算以下各对数的值:log24= , log216= , log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
(3)根据(2)的结果,我们可以归纳出:logaM+logaN=logaM N(a>0且a≠1,M>0,N>0) 请你根据幂的运算法则:am=am+n以及对数的定义证明该结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: +
+  +(﹣1)0﹣2sin45°
+(﹣1)0﹣2sin45°
(2)求满足 的x、y的正整数解.
的x、y的正整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O交△ABC的BC、AC边与D、E两点,在图中仅以没有刻度的直尺画出三角形的三条高(简单叙述你的画法).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )

A.
B.

C.

D.

相关试题

