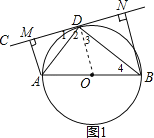
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.

(1)求证:∠ADC=∠ABD;
(2)求证:AD2=AMAB;
(3)若AM=![]() ,sin∠ABD=
,sin∠ABD=![]() ,求线段BN的长.
,求线段BN的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)连接OD,由切线的性质和圆周角定理即可得到结果;
(2)由已知条件证得△ADM∽△ABD,即可得到结论;
(3)根据三角函数和勾股定理代入数值即可得到结果.
(1)证明:连接OD,
∵直线CD切⊙O于点D,
∴∠CDO=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∵OB=OD,
∴∠3=∠4,
∴∠ADC=∠ABD;
(2)证明:∵AM⊥CD,
∴∠AMD=∠ADB=90°,
∵∠1=∠4,
∴△ADM∽△ABD,
∴![]() ,
,
∴AD2=AMAB;
(3)解:∵sin∠ABD=![]() ,
,
∴sin∠1=![]() ,
,
∵AM=![]() ,
,
∴AD=6,
∴AB=10,
∴BD=![]() =8,
=8,
∵BN⊥CD,
∴∠BND=90°,
∴∠DBN+∠BDN=∠1+∠BDN=90°,
∴∠DBN=∠1,
∴sin∠NBD=![]() ,
,
∴DN=![]() ,
,
∴BN=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A与点B(–4,–5)关于x轴对称,则A点坐标是
A.(4,–5) B.(4,5)
C.(–4,–5) D.(–4,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图乙围成一个较大的正方形.

(1)请用两种方法表示图中阴影部分面积(只需表示,不必化简);
(2)比较(1)两种结果,你能得到怎样的等量关系?
请你用(2)中得到等量关系解决下面问题:如果m﹣n=5,mn=14,求m+n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决后面的问题。
材料:我们知道,n个相同的因数a相乘
 可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)
可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)一般地,若an=b (a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4)
(1)计算以下各对数的值:log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log24、log216、log264之间又满足怎样的关系式?
(3)根据(2)的结果,我们可以归纳出:logaM+logaN=logaM N (a>0且a≠1,M>0,N>0),请你根据幂的运算法则:am=an+m以及对数的定义证明该结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
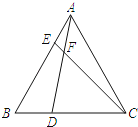
(1)求证:AD=CE;
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知PA、PB切⊙O于A、B两点,连AB,且PA,PB的长是方程x2﹣2mx+3=0的两根,AB=m.试求:
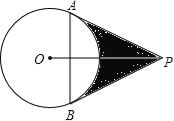
(1)⊙O的半径;
(2)由PA,PB,
 围成图形(即阴影部分)的面积.
围成图形(即阴影部分)的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】3月20日,2016长安汽车重庆国际马拉松鸣枪开跑,本届重马不仅是2016年全国马拉松锦标赛三站中的一站,同时还是2016年巴西里约奥运会马拉松唯一一站选拔赛,比赛分为全程、半程、迷你三大项目,吸引了31900多名选手参加.把数“31900”用科学记数法表示为 .
相关试题

