【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .
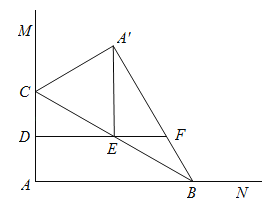
参考答案:
【答案】![]() 或
或![]()
【解析】
当△![]() 为直角三角形时,存在两种情况:
为直角三角形时,存在两种情况:
①当![]() 时,如图1,根据对称的性质和平行线可得:
时,如图1,根据对称的性质和平行线可得:![]() ,根据直角三角形斜边中线的性质得:
,根据直角三角形斜边中线的性质得:![]() ,最后利用勾股定理可得
,最后利用勾股定理可得![]() 的长;
的长;
②当![]() 时,如图2,证明
时,如图2,证明![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() .
.
解:当△![]() 为直角三角形时,存在两种情况:
为直角三角形时,存在两种情况:
①当![]() 时,如图1,
时,如图1,
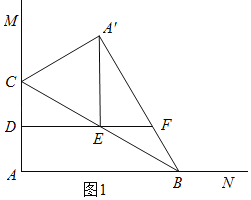
![]() △
△![]() 与
与![]() 关于
关于![]() 所在直线对称,
所在直线对称,
![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
![]() 、
、![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() △
△![]() 中,
中,![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() ,
,
由勾股定理得:![]() ,
,
![]() ;
;
②当![]() 时,如图2,
时,如图2,
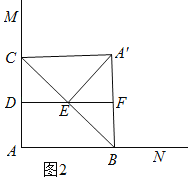
![]() ,
,
![]() ,
,
![]() △
△![]() 与
与![]() 关于
关于![]() 所在直线对称,
所在直线对称,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ;
;
综上所述,![]() 的长为
的长为![]() 或4;
或4;
故答案为:![]() 或4;
或4;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|2a+6|+(2a﹣3b+12)2=0,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A,B两点的坐标;
(2)如图2,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论;
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
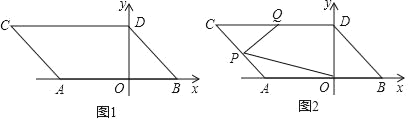
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, ,
, 为
为 边上的一点,
边上的一点, ,动点
,动点 从点
从点 出发,以每秒1个单位的速度沿着边
出发,以每秒1个单位的速度沿着边 向终点
向终点 运动,连接
运动,连接 .设点
.设点 运动的时间为
运动的时间为 秒.
秒.
(1)求
 的长;
的长;(2)当
 为多少秒时,
为多少秒时, 是直角三角形?
是直角三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第100个图中共有点的个数是

A. 15151B. 15152C. 15153D. 15154
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,坐标原点O是菱形ABCD的对称中心.边AB与x轴平行,点B(1,-2),反比例函数
 (k≠0)的图象经过A,C两点.
(k≠0)的图象经过A,C两点.
(1)求点C的坐标及反比例函数的解析式.
(2)直线BC与反比例函数图象的另一交点为E,求以O,C,E为顶点的三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.

(1)求证:AD=DE;
(2)若CE=2,求线段CD的长;
(3)在(2)的条件下,求△DPE的面积.
相关试题

