【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
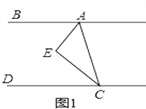
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

参考答案:
【答案】(1)AB∥CD;(2)∠BAE+![]() ∠MCD=90°;(3)∠BAC=∠PQC+∠QPC.
∠MCD=90°;(3)∠BAC=∠PQC+∠QPC.
【解析】试题分析:(1)先根据CE平分∠ACD,AE平分∠BAC,得出∠BAC=2∠EAC,∠ACD=2∠ACE,再由![]() 可知
可知![]() 故可得出结论;
故可得出结论;
(2)过E作EF∥AB,根据平行线的性质可知EF∥AB∥CD,∠BAE=∠AEF,∠FEC=∠DCE,故![]() 再由∠MCE=∠ECD,即可得出结论;
再由∠MCE=∠ECD,即可得出结论;
(3)根据AB∥CD, 可知![]()
![]() 故∠BAC=∠PQC+∠QPC.
故∠BAC=∠PQC+∠QPC.
试题解析:(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵![]()
∴![]()
∴AB∥CD;
(2) ![]()
过E作EF∥AB,
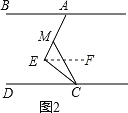
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵![]()
∴![]()
∵∠MCE=∠ECD,
∴![]()
(3)∵AB∥CD,
∴![]()
∵![]()
∴∠BAC=∠PQC+∠QPC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=
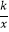 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 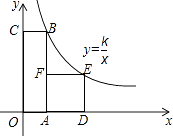
-
科目: 来源: 题型:
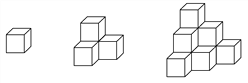
查看答案和解析>>【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
n
1
2
3
4
…
S
1
3
…
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
3
4
5
6
日销售量y(个)
20
15
12
10
(1)猜测并确定y与x之间的函数关系式,并画出图象;
(2)设经营此贺卡的销售利润为W元,求出W与x之间的函数关系式,
(3)若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3
 .分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.
.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F,过点E作EG⊥x轴于G,且EG:OG=2.求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).

(1)点C的坐标是;
(2)将△ABC沿x轴正方向平移得到△A′B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数y= 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=ax+b与直线y=x+c的交点的横坐标为1,根据图象有下列四个结论:①a<0;②c>0;③对于直线y=x+c上任意两点A(xA,yA)、B(xB,yB),若xA<xB,则yA>yB;④x>1是不等式ax+b<x+c的解集,其中正确的结论是( )

A. ①②B. ①③C. ①④D. ③④
相关试题

