【题目】如图，小强作出边长为1的第1个等边△A1B1C1 ， 计算器面积为S1 ， 然后分别取△A1B1C1三边的中点A2、B2、C1 ， 作出第2个等边△A2B2C2 ， 计算其面积为S2 ， 用同样的方法，作出第3个等边△A3B3C3 ， 计算其面积为S3 ， 按此规律进行下去，…，由此可得，第20个等边△A20B20C20的面积S20= ．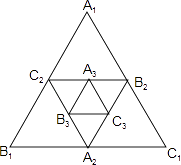

参考答案：

【答案】
【解析】解：正△A1B1C1的面积是 ，

而△A2B2C2与△A1B1C1相似，并且相似比是1：2，

则面积的比是 ，则正△A2B2C2的面积是 × ；

因而正△A3B3C3与正△A2B2C2的面积的比也是，面积是 ×（ ）2；

依此类推△AnBnCn与△An﹣1Bn﹣1Cn﹣1的面积的比是 ，第n个三角形的面积是 （ ）n﹣1．

所以第20个正△A20B20C20的面积是 ．

所以答案是： ．

【考点精析】本题主要考查了等边三角形的性质和三角形中位线定理的相关知识点，需要掌握等边三角形的三个角都相等并且每个角都是60°；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能正确解答此题．

关闭