搜索
【题目】油箱中有油30kg，油从管道中匀速流出，1小时流完，求油箱中剩余油量Q（kg）与流出时间t（分钟）间的函数关系式为__________________，自变量的范围是_____________．当Q=10kg时，t=_______________．
参考答案：
【答案】Q=30-0.5t；0≤t≤60；40
【解析】
本题考查了函数关系式及函数自变量的取值范围. 应先得到1分钟的流油量；油箱中剩油量=原来有的油量-t分流的油量，把相关数值代入即可求解．
解：∵60分钟可流完30kg油，
∴1分钟可流油30÷60=
kg，
∴t分流的油量为t，
∴Q=30-t，
∵油箱中剩余油量Q≥0，即：30-t≥0，解得：0≤t≤60，
当Q=10kg时，30-t=10，解得：t=40，
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料，并回答问题：
材料：数学课上，老师给出了如下问题．
如图1，点A、B、C均在直线l上，AB = 8，BC = 2，M是AC的中点，求AM的长．
小明的解答过程如下：
解：如图2，
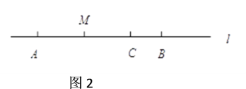
∵ AB = 8，BC = 2，
∴ AC = AB－BC = 8－2 = 6．
∵ M是AC的中点，
∴
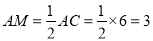（ ① ）．小芳说：“小明的解答不完整”．
问题：（1）小明解答过程中的“①”为 ；
（2） 你同意小芳的说法吗？如果同意，请将小明的解答过程补充完整；如果不同意，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2019年7月9日，北京市滴滴快车调整了价格，规定车费由“总里程费+总时长费”两部分构成，具体收费标准如下表：（注：如果车费不足起步价，则按起步价收费．）
时间段
里程费（元/千米）
时长费（元/分钟）
起步价（元）
06:00—10:00
1.80
0.80
14.00
10:00—17:00
1.45
0.40
13.00
17:00—21:00
1.50
0.80
14.00
21:00—06:00
2.15
0.80
14.00
（1）小明07:10乘快车上学，行驶里程6千米，时长10分钟，应付车费 元；
（2）小芳17:20乘快车回家，行驶里程1千米，时长15分钟，应付车费 元；
（3）小华晚自习后乘快车回家，20:45在学校上车．由于道路施工，车辆行驶缓慢，15分钟后选择另外道路，改道后速度是改道前速度的3倍，10分钟后到家，共付了车费37.4元，问从学校到小华家快车行驶了多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了美化生活环境，小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃．如图所示，矩形花圃的一边利用长10米的院墙，另外三条边用篱笆围成，篱笆的总长为32米．设AB的长为x米，矩形花圃的面积为y平方米．
（1）用含有x的代数式表示BC的长，BC= ；
（2）求y与x的函数关系式，写出自变量x的取值范围；
（3）当x为何值时，y有最大值？最大值为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，OC是∠AOB的平分线．
（1）当∠AOB = 60°时，求∠AOC的度数；
（2）在（1）的条件下，过点O作OE⊥OC，补全图形，并求∠AOE的度数；
（3）当∠AOB =
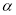时，过点O作OE⊥OC，直接写出∠AOE的度数（用含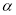代数式表示）．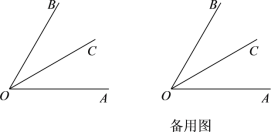
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=．
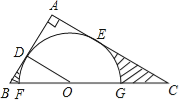
（1）求⊙O的半径OD；
（2）求证：AE是⊙O的切线；
（3）求图中两部分阴影面积的和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】古希腊毕达哥拉斯学派的数学家经常用小石子摆成各种形状来研究数学问题．
如图1，由于这些三角形是由1个，3个，6个，10个，… 小石子摆成的，所以他们称1，3，6，10，…，这些数为三边形数；类似的，如图2，他们称1，4，9，16，…，这样的数为四边形数．
（1）既是三边形数，又是四边形数，且大于1的最小正整数是 ；
（2）如果记第n个k边形小石子的个数为
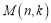（k≥3），那么易得
，
，
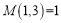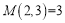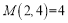．①
；
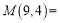；②
；
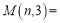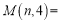；③ 如果
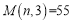，那么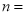
；（3）如果进一步研究发现
，
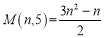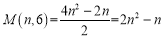，…，那么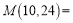
．
相关试题
