【题目】为了美化生活环境,小兰的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
(1)用含有x的代数式表示BC的长,BC= ;
(2)求y与x的函数关系式,写出自变量x的取值范围;
(3)当x为何值时,y有最大值?最大值为多少?

参考答案:
【答案】(1)32-2x;(2)y=-2x2+32x(11≤x<16);(3)当x=11时,y最大=110(m2)
【解析】试题分析:(1)、利用总长减去AB和CD就可以得出答案;(2)、根据矩形的面积计算法则得出函数解析式,根据![]() 求出取值范围;(3)、首先将函数进行配方,然后根据增减性求出最大值.
求出取值范围;(3)、首先将函数进行配方,然后根据增减性求出最大值.
试题解析:(1)、BC=32-2x;
(2)、y=x(32-2x)=![]() , 根据题意可知:
, 根据题意可知:![]()
解得:![]() ;
;
(3)、![]() ,
,
当![]() 时,y随着x的增大而减小,则根据题意可知:当x=11时,y有最大值,
时,y随着x的增大而减小,则根据题意可知:当x=11时,y有最大值,
最大值为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内有三点A、B、C.
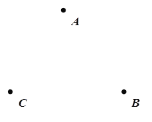
(1)作射线CA,连接BC;
(2)延长线段BC,得到射线CD,画∠ACD平分线CE;
(3)在射线CD上取一点F,使得CF = AC;
(4)在射线CE上作一点P,使PF + PA最小;
(5)第(4)步作图的依据是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,并回答问题:
材料:数学课上,老师给出了如下问题.
如图1,点A、B、C均在直线l上,AB = 8,BC = 2,M是AC的中点,求AM的长.

小明的解答过程如下:
解:如图2,
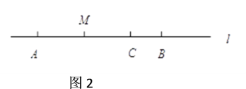
∵ AB = 8,BC = 2,
∴ AC = AB-BC = 8-2 = 6.
∵ M是AC的中点,
∴
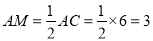 ( ① ).
( ① ).小芳说:“小明的解答不完整”.
问题:(1)小明解答过程中的“①”为 ;
(2) 你同意小芳的说法吗?如果同意,请将小明的解答过程补充完整;如果不同意,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年7月9日,北京市滴滴快车调整了价格,规定车费由“总里程费+总时长费”两部分构成,具体收费标准如下表:(注:如果车费不足起步价,则按起步价收费.)
时间段
里程费(元/千米)
时长费(元/分钟)
起步价(元)
06:00—10:00
1.80
0.80
14.00
10:00—17:00
1.45
0.40
13.00
17:00—21:00
1.50
0.80
14.00
21:00—06:00
2.15
0.80
14.00
(1)小明07:10乘快车上学,行驶里程6千米,时长10分钟,应付车费 元;
(2)小芳17:20乘快车回家,行驶里程1千米,时长15分钟,应付车费 元;
(3)小华晚自习后乘快车回家,20:45在学校上车.由于道路施工,车辆行驶缓慢,15分钟后选择另外道路,改道后速度是改道前速度的3倍,10分钟后到家,共付了车费37.4元,问从学校到小华家快车行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】油箱中有油30kg,油从管道中匀速流出,1小时流完,求油箱中剩余油量Q(kg)与流出时间t(分钟)间的函数关系式为__________________,自变量的范围是_____________.当Q=10kg时,t=_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB = 60°时,求∠AOC的度数;
(2)在(1)的条件下,过点O作OE⊥OC,补全图形,并求∠AOE的度数;
(3)当∠AOB =
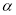 时,过点O作OE⊥OC,直接写出∠AOE的度数(用含
时,过点O作OE⊥OC,直接写出∠AOE的度数(用含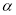 代数式表示).
代数式表示).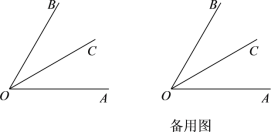
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
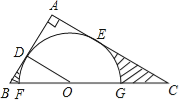
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
相关试题

