【题目】古希腊毕达哥拉斯学派的数学家经常用小石子摆成各种形状来研究数学问题.
如图1,由于这些三角形是由1个,3个,6个,10个,… 小石子摆成的,所以他们称1,3,6,10,…,这些数为三边形数;类似的,如图2,他们称1,4,9,16,…,这样的数为四边形数.

(1)既是三边形数,又是四边形数,且大于1的最小正整数是 ;
(2)如果记第n个k边形小石子的个数为![]() (k≥3),那么易得
(k≥3),那么易得![]() ,
,![]() ,
,![]() .
.
① ![]() ;
;![]() ;
;
② ![]() ;
;![]() ;
;
③ 如果![]() ,那么
,那么![]() ;
;
(3)如果进一步研究发现![]() ,
,![]() ,…,那么
,…,那么![]() .
.
参考答案:
【答案】(1)36;(2)① 6,81;②![]() ,
,![]() ;③ 10;(3)1 000.
;③ 10;(3)1 000.
【解析】
(1)图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即![]() ;图2中1、4、9、16,…,第n个图中点的个数是n2,求出能同时满足两个式子的数,即可得出结果;
;图2中1、4、9、16,…,第n个图中点的个数是n2,求出能同时满足两个式子的数,即可得出结果;
(2)由图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即![]() ;图2中1、4、9、16,…,第n个图中点的个数是n2,即可得出结果;
;图2中1、4、9、16,…,第n个图中点的个数是n2,即可得出结果;
(3)由M(n,3)![]() ,M(n,4)
,M(n,4)![]() ,M(n,5)
,M(n,5)![]() ,M(n,6)
,M(n,6)![]() ,可推断M(n,k)
,可推断M(n,k)![]() (k≥3),将M(10,24)代入即可得出结果.
(k≥3),将M(10,24)代入即可得出结果.
(1)∵四边形数点的个数是为n2,
∴除1外,分别为4,9,16,25,36,49,64,….
∵图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即三边形数点的个数是为![]() ,
,
∵4![]() 无正整数解,
无正整数解,
∴4不是三边形数.
∵9![]() 无正整数解,
无正整数解,
∴9不是三边形数.
∵16![]() 无正整数解,
无正整数解,
∴16不是三边形数.
∵25![]() 无正整数解,
无正整数解,
∴25不是三边形数.
∵36![]() ,解得:n=8,所以36是三边形数,
,解得:n=8,所以36是三边形数,
∴除1外,最小的既是三边形数又是四边形数的是36.
故答案为:36;
(2)由(1)知:M(n,3)![]() ,M(n,4)=n2;
,M(n,4)=n2;
故:①M(3,3)=![]() =6,M(9,4)=92=81;
=6,M(9,4)=92=81;
②M(n,3)![]() ,M(n,4)=n2;
,M(n,4)=n2;
③M(n,3)![]() =55,
=55,
∴n2+n-110=0,
∴(n-10)(n+11)=0,
解得:n=10或n=-11(舍去),
∴n=10.
(3)∵M(n,3)![]() ,
,
M(n,4)=n2![]() ,
,
M(n,5)![]() n2
n2![]() n
n![]() ,
,
M(n,6)=2n2﹣n![]() ,
,
∴由此变化规律可推断M(n,k)![]() (k≥3),
(k≥3),
∴M(10,24)![]() 1000.
1000.
-
科目: 来源: 题型:
查看答案和解析>>【题目】油箱中有油30kg,油从管道中匀速流出,1小时流完,求油箱中剩余油量Q(kg)与流出时间t(分钟)间的函数关系式为__________________,自变量的范围是_____________.当Q=10kg时,t=_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB = 60°时,求∠AOC的度数;
(2)在(1)的条件下,过点O作OE⊥OC,补全图形,并求∠AOE的度数;
(3)当∠AOB =
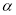 时,过点O作OE⊥OC,直接写出∠AOE的度数(用含
时,过点O作OE⊥OC,直接写出∠AOE的度数(用含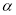 代数式表示).
代数式表示).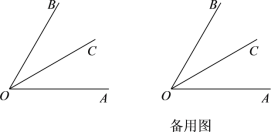
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
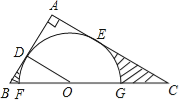
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).

(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在年产值25万元,计划今后每年增加2万元.
(1)写出年产值
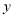 (万元)与年数
(万元)与年数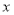 的函数关系;
的函数关系;(2)画出函数图象;
(3)求计划7年后的年产值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②当x≥1时,y随x的增大而减小;③2a+b=0;④b2﹣4ac>0;⑤
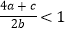 ,其中正确的个数是( )
,其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
相关试题

