搜索
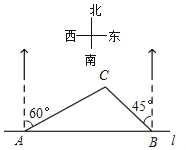
【题目】如图，在一条东西方向笔直的沿湖道路l上有A、B两个游船码头，观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向，AC＝4千米．那么码头A、B之间的距离等于_____千米．（结果保留根号）
参考答案：
【答案】（2
+2）
【解析】
作CD⊥AB于点D，在Rt△ACD中利用三角函数求得CD、AD的长，然后在Rt△BCD中求得BD的长，即可得到码头A、B之间的距离．
如图，作CD⊥AB于点D．
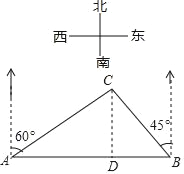
∵在Rt△ACD中，∠CAD＝90°﹣60°＝30°，
∴CD＝ACsin∠CAD＝4×
＝2（km），AD＝ACcos30°＝4×
＝2（km），
∵Rt△BCD中，∠CDB＝90°，∠CBD＝45°，
∴BD＝CD＝2（km），
∴AB＝AD+BD＝2+2（km），
故答案是：（2+2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在50包型号为L的衬衫的包裹中混进了型号为M的衬衫，每包20件衬衫，每包中混入的M号衬衫数如表：
M号衬衫数
0
1
4
5
7
9
10
11
包数
7
3
10
15
5
4
3
3
根据以上数据，选择正确选项（ ）.
A．M号衬衫一共有47件
B．从中随机取一包，包中L号衬衫数不低于9是随机事件
C．从中随机取一包，包中L号衬衫数不超过4的概率为0.26
D．将50包衬衫混合在一起，从中随机拿出一件衬衫，恰好是M号的概率为0.252
-
科目： 来源： 题型：
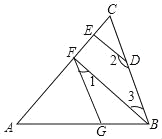
查看答案和解析>>【题目】如图，DE⊥AC于点E，BF⊥AC于点F，∠1+∠2＝180°，求证：∠AGF＝∠ABC．
试将下面的证明过程补充完整(填空)：
证明：∵DE⊥AC，BF⊥AC(已知)
∴∠AFB＝∠AED＝90°(_______)
∴BF∥DE(同位角相等，两直线平行)，
∴∠2+∠3＝180°(两直线平行，同旁内角互补)，
又∵∠1+∠2＝180°(已知)，
∴∠1＝______，(同角的补角相等)
∴GF∥_____(内错角相等，两直线平行)，
∴∠AGF＝∠ABC．(______)
-
科目： 来源： 题型：
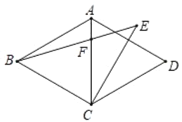
查看答案和解析>>【题目】如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝_____°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别
成绩x分
频数
人数
第1组
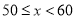
6
第2组
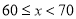
8
第3组
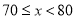
14
第4组
a
第5组
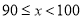
10
请结合图表完成下列各题：
求表中a的值； 
频数分布直方图补充完整；
若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．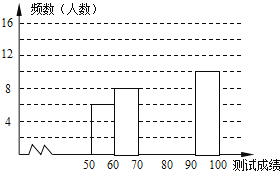
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线过A（﹣1，5），P（2，a），B（3，﹣3）．
（1）求直线AB的解析式和a的值；
（2）求△AOP的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，过B点作BM⊥AC于点E，交CD于点M，过D点作DN⊥AC于点F，交AB于点N．
（1）求证：四边形BMDN是平行四边形；
（2）已知AF=12，EM=5，求AN的长．
相关试题
