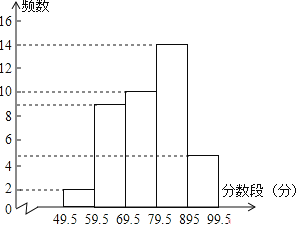
【题目】九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
分数段(分) | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
组中值(分) | 54.5 | 64.5 | 74.5 | 84.5 | 94.5 |
频数 | a | 9 | 10 | 14 | 5 |
所占百分比 | 5% | 22.5% | 25.0% | 35.0% | b |
(1)频数分布表中a=______,b=______;
(2)画频数分布直方图;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
参考答案:
【答案】(1) 2,0.125;(2)作图见解析;(3) 1050元.
【解析】试题分析:(1)由成绩频数分布表可以看出,b=1-0.05-0.225-0.25-0.35=0.125;由已知组的频数占总数的百分比及频数求出总数,用总数乘0.050求出a的值;
(2)由数据补全直方图;
(3)由表得,有29名同学获得一等奖或二等奖;设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得关系式15x+10(29-x)=335可求得x的值;再根据关系式50x+30(29-x)可求得获得的奖金.
试题解析:解:(1)频数分布表中,由于![]() ×100%=40(人),则a=40×0.050=2(人),
×100%=40(人),则a=40×0.050=2(人),
b=1-0.05-0.225-0.25-0.35=0.125;
(2)如图所示:
(3)由表得,有29名同学获得一等奖或二等奖,
设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意,得
15x+10(29-x)=335,
解得x=9,
∴50x+30(29-x)=1050.
所以他们得到的奖金是1050元.
-
科目: 来源: 题型:
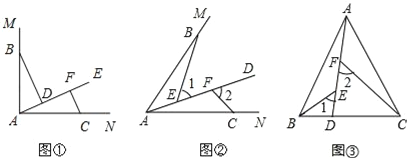
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2a与1﹣a互为相反数,则a=_____.如果|2a+3|=1,那么a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学课上,老师在黑板上画了如图图形,并写下了四个等式:
①BD=CA,②AB=DC,③∠B=∠C,④∠BAE=∠CDE.
要求同学从这四个等式中选出两个作为条件,推出AE=DE.请你试着完成老师提出的要求,并说明理由.(写出一种即可)
已知:____(请填写序号),求证:AE=DE.
证明:

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式23>7+5x的正整数解的个数是( )
A.1个
B.无数个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间 x(单位:h)变化的图象如图所示,

根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】|﹣1|的相反数是( )
A.1B.0C.﹣1D.±1
相关试题

