【题目】请根据图中信息回答下列问题:

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某人想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
参考答案:
【答案】(1)一个暖瓶70元,一个水杯30元;(2)到乙家商场购买更合算.
【解析】
(1)根据题意设一个暖瓶x元,一个水杯y元,列方程组解答即可.
(2)分别计算到两商场购买的价钱,再比较即可解答.
解:(1)设一个暖瓶x元,一个水杯y元,
根据题意得:![]() ,
,
解得:![]() .
.
答:一个暖瓶70元,一个水杯30元
(2)若到甲商场购买,则所需的钱数为:(4×70+15×30)×90%=657(元),
若到乙商场购买,则所需的钱数为:4×70+(15﹣4)×30=610(元).
∵657>610,
∴到乙家商场购买更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△OAB中,OA=OB,C为AB中点,以O圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF、CF,CF与OA交于点G.
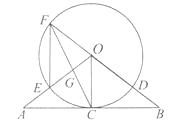
(1)求证:直线AB是⊙O的切线;
(2)求证:OD·EG=OG·EF;
(3)若AB=8,BD=2,求⊙O的半径. -
科目: 来源: 题型:
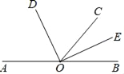
查看答案和解析>>【题目】填空,完成下列说理过程
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx-3经过A(-1,0)、B(3,0)两点,与y轴交于C点,
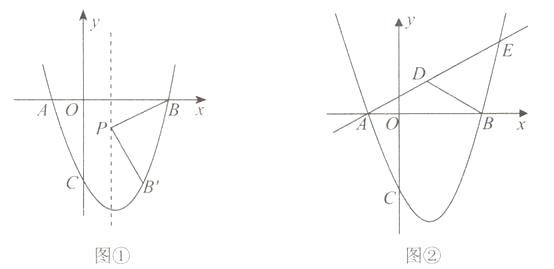
(1)求抛物线的解析式;
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标;
(3)如图②,直线y=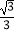 x+
x+ 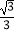 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市统计局发布的2016年《深圳市气候数据每日观测记录》显示,2016年12月26—21日这六天的平均相对湿度(百分数)分别是58,50,45,54,64,82.对于这组数据,以下说法正确的是( )
A.平均数是59
B.中位数是56
C.众数是82
D.方差是37 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:
 =
= (a≠0),即a的负P次幂等于a的p次幂的倒数.例:
(a≠0),即a的负P次幂等于a的p次幂的倒数.例: =
=
(1)计算:
 =__;
=__; =__;
=__;(2)如果
 =
= ,那么p=__;如果
,那么p=__;如果 =
= ,那么a=__;
,那么a=__;(3)如果
 =
= ,且a、p为整数,求满足条件的a、p的取值.
,且a、p为整数,求满足条件的a、p的取值.
相关试题

