【题目】如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在![]() 处.若AB=3,BC=9,则折痕EF的长为()
处.若AB=3,BC=9,则折痕EF的长为()
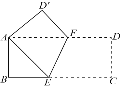
A. ![]() B. 4 C. 5 D.
B. 4 C. 5 D. ![]()
参考答案:
【答案】A
【解析】
根据翻折的性质可得AE=EC,∠AEF=∠CEF,设AE=x,表示出BE.在Rt△ABE中,利用勾股定理列方程求出x,根据两直线平行,内错角相等可得∠AFE=∠CEF,从而得到∠AEF=∠AFE,根据等角对等边可得AF=AE,过点E作EG⊥AD于G,求出AG、GF,再利用勾股定理列式计算即可得解.
∵矩形ABCD沿EF折叠,点C落在A处,∴AE=EC,∠AEF=∠CEF,
设AE=x,则BE=BC﹣EC=9﹣x,
在Rt△ABE中,根据勾股定理得:AB2+BE2=AE2,
即32+(9﹣x)2=x2,
解得:x=5,
所以,AE=5,BE=9﹣5=4,
∵矩形对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AF=AE=5,
过点E作EG⊥AD于G,则四边形ABEG是矩形,∴AG=BE=4,
GF=AF﹣AG=5﹣4=1,
在Rt△EFG中,根据勾股定理得:EF=![]() =
=![]() =
=![]() .
.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )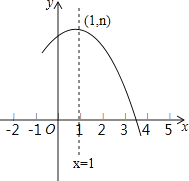
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 )×(﹣36); (2)[2﹣5×(﹣
)×(﹣36); (2)[2﹣5×(﹣ )2]÷(﹣
)2]÷(﹣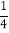 );
);(3)1
 ×
× ﹣(﹣
﹣(﹣  )×2
)×2 +(﹣
+(﹣  )÷1
)÷1  ; (4)﹣14﹣[1﹣(1﹣0.5×
; (4)﹣14﹣[1﹣(1﹣0.5×  )×6]
)×6](5)
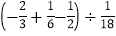 ; (6)-22+(1-
; (6)-22+(1-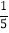 ×0.2)÷(-2)3.
×0.2)÷(-2)3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为
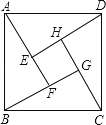
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并解答:
规定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 个 a)
(1)(2×3)2= ,22×32= ,你发现(2× 3)2 的值与 22×32 的值 .
(2)(2×3)3= ,23×33= ,你发现(2×3)3 的值与 23×33 的值 .
由此,我们可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)题结论计算(﹣2)2018×(﹣
 )2019 的值.
)2019 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一种“24 点”游戏,其游戏规则是:任取一副扑克牌,我们约定A 为 1,J,Q,K 分别为 11、12、13,并规定红色牌为正,黑色牌为负,任取 4 张牌,将这 4 张牌的牌面所表示的数进行加减乘除四则运算(每个数用且只用 1 次),使其结果等于 24.
例如,取 4 张牌为:红桃 A,红桃 2,方块 3,方块 4,可作运算(1+2+3)×4 =24.
[注意上述运算与 4×(1+2+3)=24 应视作相同方法的运算]
现有 4 张扑克牌分别为红桃 3、黑桃 6、方块 4、方块 10,运用上述规则写出 3种不同的运算式:
(1) ;
(2) ;
(3) .
(4)另有 4 张扑克牌分别为红桃 3,黑桃 5,梅花 J,方块 7,可通过运算式 ,使其结果等于 24.
相关试题

