【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为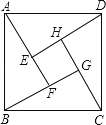
参考答案:
【答案】![]()
【解析】解:设小正方形EFGH面积是a2 , 则大正方形ABCD的面积是13a2 , ∴小正方形EFGH边长是a,则大正方形ABCD的面积是 ![]() a,
a,
∵图中的四个直角三角形是全等的,
∴AE=DH,
设AE=DH=x,
在Rt△AED中,AD2=AE2+DE2 ,
即13a2=x2+(x+a)2
解得:x1=2a,x2=﹣3a(舍去),
∴AE=2a,DE=3a,
∴tan∠ADE= ![]() ,故答案为:
,故答案为: ![]() .
.
小正方形EFGH面积是a2 , 则大正方形ABCD的面积是13a2 , 则小正方形EFGH边长是a,则大正方形ABCD的面积是 ![]() a,设AE=DH=x,利用勾股定理求出x,最后利用熟记函数即可解答.此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边,进一步运用锐角三角函数的定义求解.
a,设AE=DH=x,利用勾股定理求出x,最后利用熟记函数即可解答.此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边,进一步运用锐角三角函数的定义求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )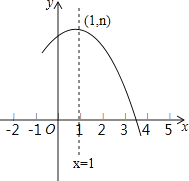
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 )×(﹣36); (2)[2﹣5×(﹣
)×(﹣36); (2)[2﹣5×(﹣ )2]÷(﹣
)2]÷(﹣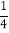 );
);(3)1
 ×
× ﹣(﹣
﹣(﹣  )×2
)×2 +(﹣
+(﹣  )÷1
)÷1  ; (4)﹣14﹣[1﹣(1﹣0.5×
; (4)﹣14﹣[1﹣(1﹣0.5×  )×6]
)×6](5)
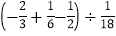 ; (6)-22+(1-
; (6)-22+(1-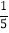 ×0.2)÷(-2)3.
×0.2)÷(-2)3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在
 处.若AB=3,BC=9,则折痕EF的长为()
处.若AB=3,BC=9,则折痕EF的长为()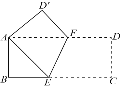
A.
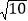 B. 4 C. 5 D.
B. 4 C. 5 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并解答:
规定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 个 a)
(1)(2×3)2= ,22×32= ,你发现(2× 3)2 的值与 22×32 的值 .
(2)(2×3)3= ,23×33= ,你发现(2×3)3 的值与 23×33 的值 .
由此,我们可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)题结论计算(﹣2)2018×(﹣
 )2019 的值.
)2019 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一种“24 点”游戏,其游戏规则是:任取一副扑克牌,我们约定A 为 1,J,Q,K 分别为 11、12、13,并规定红色牌为正,黑色牌为负,任取 4 张牌,将这 4 张牌的牌面所表示的数进行加减乘除四则运算(每个数用且只用 1 次),使其结果等于 24.
例如,取 4 张牌为:红桃 A,红桃 2,方块 3,方块 4,可作运算(1+2+3)×4 =24.
[注意上述运算与 4×(1+2+3)=24 应视作相同方法的运算]
现有 4 张扑克牌分别为红桃 3、黑桃 6、方块 4、方块 10,运用上述规则写出 3种不同的运算式:
(1) ;
(2) ;
(3) .
(4)另有 4 张扑克牌分别为红桃 3,黑桃 5,梅花 J,方块 7,可通过运算式 ,使其结果等于 24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜.

相关试题

