【题目】在ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
参考答案:
【答案】D
【解析】解:①如图1,在ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF=2AB﹣EF=8,
∴AB=5;
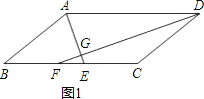
②在ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=2,
∴BC=BE+CF=2AB+EF=8,
∴AB=3;
综上所述:AB的长为3或5.
故选D.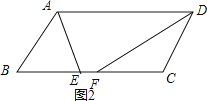
根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据已知条件得到四边形ABCD是平行四边形,根据平行四边形的性质得到AB=CD,AD=BC,即可得到结论.本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数 a,b 在数轴上的位置如图所示,则下列各式中一定成立的是( )
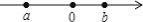
A. ﹣a>b B. a+b>0 C. a﹣b>a+b D. |a|+|b|<|a+b|
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )
成绩(分)
27
28
30
人数
2
3
1
A.28,28,1
B.28,27.5,1
C.3,2.5,5
D.3,2,5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )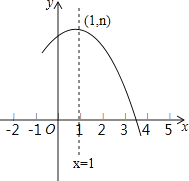
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 )×(﹣36); (2)[2﹣5×(﹣
)×(﹣36); (2)[2﹣5×(﹣ )2]÷(﹣
)2]÷(﹣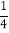 );
);(3)1
 ×
× ﹣(﹣
﹣(﹣  )×2
)×2 +(﹣
+(﹣  )÷1
)÷1  ; (4)﹣14﹣[1﹣(1﹣0.5×
; (4)﹣14﹣[1﹣(1﹣0.5×  )×6]
)×6](5)
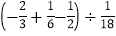 ; (6)-22+(1-
; (6)-22+(1-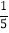 ×0.2)÷(-2)3.
×0.2)÷(-2)3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在
 处.若AB=3,BC=9,则折痕EF的长为()
处.若AB=3,BC=9,则折痕EF的长为()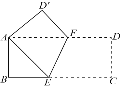
A.
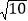 B. 4 C. 5 D.
B. 4 C. 5 D. 
相关试题

