【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
参考答案:
【答案】(1)3个单位长度/秒, 2个单位长度/秒;(2)见解析;(3)![]() 、
、![]() 、11或19秒.
、11或19秒.
【解析】
(1)设点B的速度为2x个单位长度/秒,则点A的速度为3x个单位长度/秒,根据速度和×时间=二者间的距离,即可得出关于x的一元一次方程,解之即可得出结论;
(2)由路程=速度×时间结合运动方向可得出运动到3秒钟时点A、B所表示的数,再将其标记在数轴上即可;
(3)设运动的时间为t秒,由A、B两点的速度关系可分A、B两点向数轴正方向运动及A、B两点相向而行两种情况,根据A、B两点的运动速度结合A、B两点之间相距4个单位长度,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论.
解:(1)设点B的速度为2x个单位长度/秒,则点A的速度为3x个单位长度/秒,
根据题意得:3×(2x+3x)=15,
解得:x=1,
∴3x=3,2x=2.
答:动点A的运动速度为3个单位长度/秒,动点B的运动速度为2个单位长度/秒.
(2)3×3=9,2×3=6,
∴运动到3秒钟时,点A表示的数为﹣9,点B表示的数为6.
(3)设运动的时间为t秒.
当A、B两点向数轴正方向运动时,有|3t﹣2t﹣15|=4,
解得:t1=11或t2=19;
当A、B两点相向而行时,有|15﹣3t﹣2t|=4,
解得:t3=![]() 或t4=
或t4=![]() .
.
答:经过![]() 、
、![]() 、11或19秒,A、B两点之间相距4个单位长度.
、11或19秒,A、B两点之间相距4个单位长度.
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】科学考察队的一辆越野车需要穿越650千米的沙漠,但这辆车每次装满汽油最多只能行驶600千米,队长想出一个方法,在沙漠中设一个储油点
 ,越野车装满油从起点
,越野车装满油从起点 出发,到储油点
出发,到储油点 时从车中取出部分油放进
时从车中取出部分油放进 储油点,然后返回出发点
储油点,然后返回出发点 ,加满油后再开往
,加满油后再开往 ,到
,到 储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数
中位数
方差
甲
8
8
乙
8
8
2.2
丙
6
3
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017湖南省益阳市)在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线
 的图象上有一对“互换点”A、B,其中点A在反比例函数
的图象上有一对“互换点”A、B,其中点A在反比例函数 的图象上,直线AB经过点P(
的图象上,直线AB经过点P( ,
, ),求此抛物线的表达式.
),求此抛物线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:

将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC=
 b2+
b2+ ab.
ab.又∵S四边形ADCB=S△ADB+S△DCB=
 c2+
c2+ a(b﹣a)
a(b﹣a)∴
 b2+
b2+ ab=
ab= c2+
c2+ a(b﹣a)
a(b﹣a)∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2
证明:连结______,过点B作________,则____________.
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=____________.
又∵S五边形ACBED=______________=
 ab+
ab+ c2+
c2+ a(b﹣a),
a(b﹣a),∴___________________=
 ab+
ab+ c2+
c2+ a(b﹣a),
a(b﹣a),∴a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1< <2,所以
<2,所以 的整数部分为1,将
的整数部分为1,将 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分 ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:(1)
 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;(2)
 的整数部分是______,小数部分是_____;
的整数部分是______,小数部分是_____;(3)若设
 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣ y的值.
y的值. -
科目: 来源: 题型:
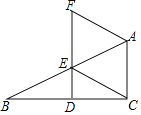
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
相关试题

