Question

【题目】如图，E为正方形ABCD对角线BD上的一点，且BE＝BC＝1．

（1）求∠DCE的度数；

（2）点P在EC上，作PM⊥BD于M，PN⊥BC于N，求PM＋PN的值．

Answer 1

【答案】（1）22．5°，（2）．

【解析】

试题分析：（1）由正方形的性质得到，∠BCD=90°，∠DBC=45°，推出AB=BE，根据三角形的内角和定理求出∠BCE=∠BEC=67．5°，根据∠DCE=∠DCB-∠BCE即可求出答案．

（2）连接BP，作EF⊥BC于F，则∠EFB=90°，得出△BEF是等腰直角三角形，从而求得BF=EF=，然后根据S△BPE+S△BPC=S△BEC，求得PM+PN=EF，即可求得．

试题解析：（1）在正方形ABCD中，∠BCD=90°，∠DBC=45°，

∵BE=BC，

∴AB=BE，

∴∠BCE=∠BEC=（180°-∠DBC）=67．5°，

∴∠DCE=∠DCB-∠BCE=90°-67．5°=22．5°，

（2）连接BP，作EF⊥BC于F，则∠EFB=90°，

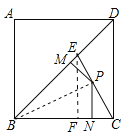
∵∠EBF=45°，

∴△BEF是等腰直角三角形，

∵BE=BC=1，

∴BF=EF=，

∵PM⊥BD，PN⊥BC，

∴S△BPE+S△BPC=S△BEC，

即BEPM+BCPN=BCEF，

∵BE=BC，

∴PM+PN=EF=．