Question

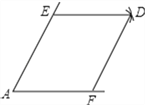
【题目】如图，在ABCD中，点E是BC的中点，连接并延长DE交AB的延长线于点F．
（1）求证：△CDE≌△BFE；
（2）若CD=3cm，请求出AF的长度．

Answer 1

【答案】
（1）证明：∵E是BC的中点，

∴CE=BE，

∵四边形ABCD是平行四边形，

∴AB∥CD，AB=CD，

∴∠DCB=∠FBE，

在△CDE和△BFE中， ，

∴△CDE≌△BFE（ASA）

（2）解：由（1）得△CDE≌△BFE，

∴CD=BF=3cm，

∴AB=3cm，

∴AF=AB+BF=6cm

【解析】（1）根据线段中点的定义可得CE=BE，根据平行四边形的对边平行且相等可得AB∥CD，AB=CD，再根据两直线平行，内错角相等可得∠DCB=∠FBE，然后利用“角边角”证明△CED和△BEF全等；（2）根据全等三角形对应边相等可得CD=BF，从而得解．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)．