Question

【题目】如图，∠1+∠2=180°，∠A=∠C，DA平分∠BDF．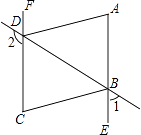

（1）AE与FC会平行吗？说明理由；
（2）AD与BC的位置关系如何？为什么？
（3）BC平分∠DBE吗？为什么．

Answer 1

【答案】
（1）解：平行．理由如下：

∵∠1+∠2=180°，∠2+∠CDB=180°（邻补角定义），

∴∠1=∠CDB，

∴AE∥FC（ 同位角相等两直线平行）

（2）解：平行．理由如下：

∵AE∥CF，

∴∠C=∠CBE（两直线平行，内错角相等），

又∵∠A=∠C，

∴∠A=∠CBE，

∴AD∥BC（同位角相等，两直线平行）

（3）解：平分．理由如下：

∵DA平分∠BDF，

∴∠FDA=∠ADB，

∵AE∥CF，AD∥BC，

∴∠FDA=∠A=∠CBE，∠ADB=∠CBD，

∴∠EBC=∠CBD，

∴BC平分∠DBE．

【解析】由∠1+∠2=180°，∠2+∠CDB=180°（邻补角定义），得到∠1=∠CDB，得到AD∥BC（同位角相等，两直线平行）；（2）由AE∥CF，得到∠C=∠CBE（两直线平行，内错角相等），又∠A=∠C，得到∠A=∠CBE，得到AD∥BC（同位角相等，两直线平行）；（3）由DA平分∠BDF，得到∠FDA=∠ADB，因为AE∥CF，AD∥BC，所以∠FDA=∠A=∠CBE，∠ADB=∠CBD，得到∠EBC=∠CBD.
【考点精析】根据题目的已知条件，利用平行线的判定的相关知识可以得到问题的答案，需要掌握同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行．