【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数. 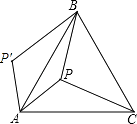
参考答案:
【答案】解:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2 ,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.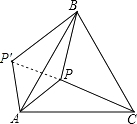
【解析】先根据等边三角形的性质得AB=AC,∠BAC=60°,再利用旋转的性质得∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,于是可判断△AP′P为等边三角形,得到PP′=AP=5,∠APP′=60°,接着根据勾股定理的逆定理证明△BPP′为直角三角形,且∠BPP′=90°,然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数.
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,有
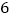 张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是( )
张写有实数的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图②摆放,从中任意翻开两张都是无理数的概率是( )
A.
 B.
B.  C.
C.  D.
D. 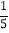
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 ,
, 随
随 增大而增大,它的图象经过点
增大而增大,它的图象经过点 且与
且与 轴的夹角为
轴的夹角为 ,
, 确定这个一次函数的解析式;
确定这个一次函数的解析式; 假设已知中的一次函数的图象沿
假设已知中的一次函数的图象沿 轴平移两个单位,求平移以后的直线及直线与
轴平移两个单位,求平移以后的直线及直线与 轴的交点坐标.
轴的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
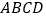 的边长为
的边长为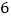 ,点
,点 在边
在边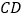 上,且
上,且 ,将
,将 沿
沿 对折至
对折至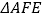 ,延长
,延长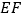 交边
交边 于点
于点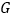 ,连接
,连接 、
、 ,则下列结论:①
,则下列结论:①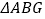 ≌
≌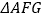 ;②
;②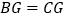 ;③
;③ ∥
∥ ;④
;④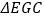 与
与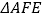 的面积相等;⑤
的面积相等;⑤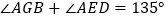 ,其中正确的个数是( )
,其中正确的个数是( )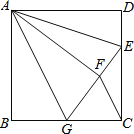
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
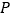 是
是 的角平分线上的一点,
的角平分线上的一点, ,
,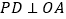 ,
,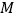 是
是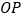 的中点,点
的中点,点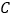 是
是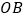 上的一个动点,若
上的一个动点,若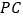 的最小值为
的最小值为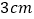 ,则
,则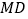 的长度为____
的长度为____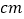 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC,CE.
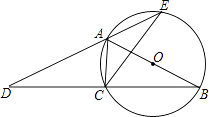
(1)求证:∠B=∠D;
(2)若AB=13,BC﹣AC=7,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于__________.

相关试题

