【题目】已知点A(x1,y1),B(x2,y2)在直线y=kx+b上,且直线经过第一,二,三象限,当x1>x2时,y1与y2的大小关系是_____.
参考答案:
【答案】y1>y2
【解析】
直接利用一次函数的性质分析得出答案.
解:∵直线经过第一,二,三象限,
∴k>0,b>0,
∴y随x值的增大而增大,
∴当x1>x2时,y1>y2,
∴y1>y2,
故答案为y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是一个三角形的三条边长,则化简|a+b-c|-|a-b-c|=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
-
科目: 来源: 题型:
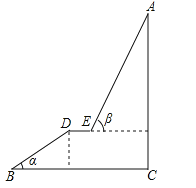
查看答案和解析>>【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,
 (C与O重合,D点在数轴的正半轴上)
(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF 平分
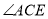 ,则
,则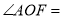 _________;
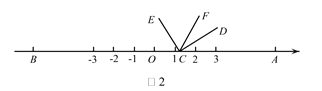
_________;(2)如图2,将
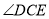 沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点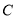 逆时针旋转30t度,作
逆时针旋转30t度,作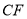 平分
平分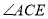 ,此时记
,此时记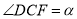 .
.①当t=1时,
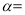 _______;
_______;②猜想
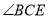 和
和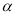 的数量关系,并证明;
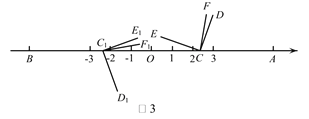
的数量关系,并证明;(3)如图3,开始
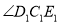 与
与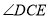 重合,将
重合,将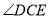 沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点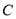 逆时针旋转30t度,作
逆时针旋转30t度,作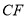 平分
平分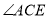 ,此时记
,此时记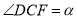 ,与此同时,将
,与此同时,将 沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点
沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点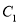 顺时针旋转30t度,作
顺时针旋转30t度,作 平分
平分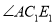 ,记
,记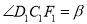 ,若
,若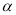 与
与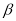 满足
满足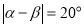 ,请直接写出t的值为_________.
,请直接写出t的值为_________.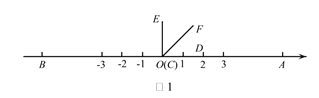
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个多边形的所有内角的和为1800°,且两个多边形的边数之比为2:5,求这两个多边形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了有理数的乘法后,老师给同学们布置这样一道题目:计算49
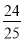 ×(–5),看谁算的又快又对,有三位同学的解法如下:
×(–5),看谁算的又快又对,有三位同学的解法如下:小军:原式 =(49 +
 )×(–5)= 49×(–5)+
)×(–5)= 49×(–5)+ 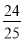 ×(–5)
×(–5)=–245–4
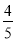 =–249
=–249 ;
;小明:原式 = –
 × 5 = –
× 5 = –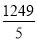 = – 249
= – 249 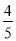 ;
;小丽:原式 =(49 +
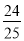 )×(-5)=(50 -1 +
)×(-5)=(50 -1 + 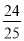 )×(-5)
)×(-5)=(50 -
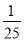 )×(-5)= 50 ×(-5)+( -
)×(-5)= 50 ×(-5)+( - 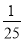 ) ×(-5)
) ×(-5)= –250 +
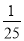 = –249
= –249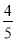 ;
;(1)对于以上三种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,用你认为最合适的方法计算:
19
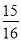 ×(– 8)
×(– 8)
相关试题

