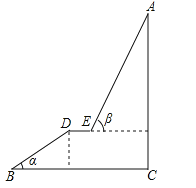
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
参考答案:
【答案】155.8.
【解析】
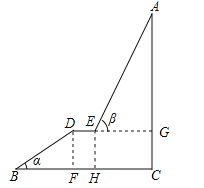
试题分析:先求出DF的长,得到CG的长,再求出AG的长,求和得到答案.
试题解析:∵cos∠DBF=![]() ,∴BF=60×0.85=51,FH=DE=9,∴EG=HC=110﹣51﹣9=50,∵tan∠AEG=
,∴BF=60×0.85=51,FH=DE=9,∴EG=HC=110﹣51﹣9=50,∵tan∠AEG=![]() ,∴AG=50×2.48=124,∵sin∠DBF=
,∴AG=50×2.48=124,∵sin∠DBF=![]() ,∴DF=60×0.53=31.8,∴CG=31.8,∴AC=AG+CG=124+31.8=155.8.
,∴DF=60×0.53=31.8,∴CG=31.8,∴AC=AG+CG=124+31.8=155.8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)、求证:DE⊥AG;
(2)、如图2,正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°),得到正方形OE′F′G′;
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为2,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是一个三角形的三条边长,则化简|a+b-c|-|a-b-c|=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x1,y1),B(x2,y2)在直线y=kx+b上,且直线经过第一,二,三象限,当x1>x2时,y1与y2的大小关系是_____.
-
科目: 来源: 题型:
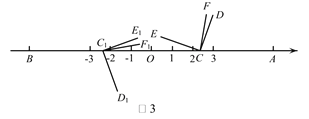
查看答案和解析>>【题目】如图1,在数轴上A,B两点对应的数分别是6,-6,
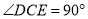 (C与O重合,D点在数轴的正半轴上)
(C与O重合,D点在数轴的正半轴上)(1)如图1,若CF 平分
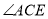 ,则
,则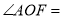 _________;
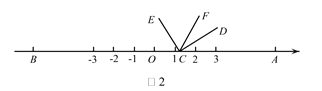
_________;(2)如图2,将
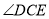 沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点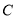 逆时针旋转30t度,作
逆时针旋转30t度,作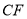 平分
平分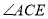 ,此时记
,此时记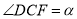 .
.①当t=1时,
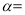 _______;
_______;②猜想
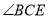 和
和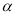 的数量关系,并证明;
的数量关系,并证明;(3)如图3,开始
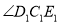 与
与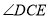 重合,将
重合,将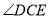 沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点
沿数轴的正半轴向右平移t(0<t<3)个单位,再绕点顶点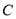 逆时针旋转30t度,作
逆时针旋转30t度,作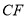 平分
平分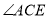 ,此时记
,此时记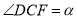 ,与此同时,将
,与此同时,将 沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点
沿数轴的负半轴向左平移t(0<t<3)个单位,再绕点顶点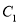 顺时针旋转30t度,作
顺时针旋转30t度,作 平分
平分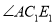 ,记
,记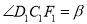 ,若
,若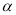 与
与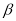 满足
满足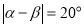 ,请直接写出t的值为_________.
,请直接写出t的值为_________.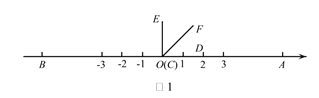
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个多边形的所有内角的和为1800°,且两个多边形的边数之比为2:5,求这两个多边形的边数.
相关试题

