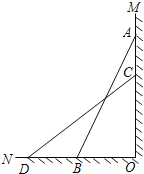
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?
参考答案:
【答案】(1)梯子顶端距地面12m高;(2)滑动不等于4m,理由见解析;(3)AB上的中点O到墙角O的距离总是定值,因为直角三角形斜边上的中线等于斜边的一半.
【解析】
(1)在中利用勾股定理求得AO的长即可;
(2)在梯子长度不变的情况下,求出DO的长后减去BO的长求得BD即可作出判断.
(1)∵AO⊥DO,∴AO=12m,
∴梯子顶端距地面12m高;
(2)滑动不等于4m,
∵AC=4m,
∴OC=AO-AC=8m,
∴OD=![]() m,
m,
∴BD=OD-OB=![]() 5>4,
5>4,
∴滑动不等于4m;
(3)AB上的中点O到墙角O的距离总是定值,因为直角三角形斜边上的中线等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.

(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( )

A.3对
B.4对
C.5对
D.6对 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2+bx+c的图象与x轴交于两点,与y轴的正半轴交于一点,且对称轴为x=1,则下列说法正确的是( )
A.二次函数的图象与x轴的交点位于y轴的两侧
B.二次函数的图象与x轴的交点位于y轴的右侧
C.其中二次函数中的c>1
D.二次函数的图象与x轴的一个交于位于x=2的右侧 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于频率与概率有下列几种说法:( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为
 ”表示每抛两次就有一次正面朝上;
”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为
 ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在 附近,正确的说法是
附近,正确的说法是A.①④ B.②③ C.②④ D.①③
-
科目: 来源: 题型:
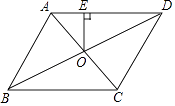
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE= .
相关试题

