【题目】如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( ) 
A.3对
B.4对
C.5对
D.6对
参考答案:
【答案】D
【解析】解:∵四边形ABCD为矩形,其矩形的对角线相等且相互平分, ∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△AOE≌△COF(ASA),△DOE≌△BOF(ASA),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共有6对.
故选D
【考点精析】根据题目的已知条件,利用矩形的性质的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A,B,O,C为数轴上四点,点A对应数a(a<﹣2),点O对应0,点C对应3,AB=2 (AB表示点A到点B的距离).
(1)填空:点C到原点O的距离 ,:点B对应的数 .(用含有a的式子)
(2)如图2,将一刻度尺放在数轴上,刻度尺上“6cm”和“8.7cm”分别对应数轴上的点O和点C,若BC=5,求a的值和点A在刻度尺上对应的刻度.
(3)如图3,在(2)的条件下,点A以1单位长度/秒的逮度向右运动,同时点C向左运动,若运动3秒时,点A和点C到原点D的距离相等,求点C的运动速度.)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AB=10,BC=6,
(1)计算AC的长度;
(2)计算AB边上的中线CD的长度.
(3)计算AB边上的高CE的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.

(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=
 ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
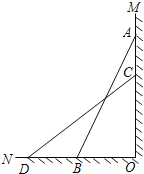
查看答案和解析>>【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2+bx+c的图象与x轴交于两点,与y轴的正半轴交于一点,且对称轴为x=1,则下列说法正确的是( )
A.二次函数的图象与x轴的交点位于y轴的两侧
B.二次函数的图象与x轴的交点位于y轴的右侧
C.其中二次函数中的c>1
D.二次函数的图象与x轴的一个交于位于x=2的右侧
相关试题

