搜索
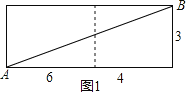
【题目】如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）
A. 
cm B. 
cm C. 
cm D. 9cm
参考答案：
【答案】C
【解析】
本题中蚂蚁要跑的路径有三种情况，知道当蚂蚁爬的是一条直线时，路径才会最短．蚂蚁爬的是一个长方形的对角线．展开成平面图形，根据两点之间线段最短，可求出解．
解：如图1，当爬的长方形的长是(4+6)=10，宽是3时，需要爬行的路径的长=
=
cm；
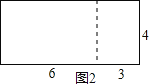
如图2，当爬的长方形的长是(3+6)=9，宽是4时，需要爬行的路径的长=
=
cm；
如图3，爬的长方形的长是(3+4)=7时，宽是6时，需要爬行的路径的长=
=
cm.
所以要爬行的最短路径的长cm.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是工人师傅用同一种材料制成的金属框架，已知
，
，
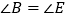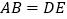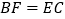，其中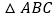
的周长为24cm，
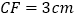，则制成整个金属框架所需这种材料的总长度为( )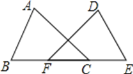
A. 45cm B. 48cm C. 51cm D. 54cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一根24cm的筷子置于底面直径为15cm，高为8cm的圆柱形水杯中，设筷子露在杯子外面的长度为hcm，则h的取值范围是（ ）
A. h≤17 B. h≥8 C. 15≤h≤16 D. 7≤h≤16
-
科目： 来源： 题型：
查看答案和解析>>【题目】一位无线电爱好者把天线杆设在接收效果最佳的矩形屋顶之上．然后，他从杆顶到屋顶四角之间安装固定用的支撑线．有两根相对的支撑线分别长7米和4米，另一根长1米，则最后一根的长度应为（ ）
A. 8米 B. 9米 C. 10米 D. 12米
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AB为直径作半圆O交BC于点D，过点D作DE⊥AC，垂足为E．
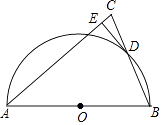
（1）求证：DE是⊙O的切线；
（2）若CE=1，BC=6，求半圆O的半径的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】一组对边平行，另一组对边相等且不平行的四边形叫做等腰梯形．
（1）类比研究
我们在学完平行四边形后，知道可以从对称性、边、角和对角线四个角度对四边形进行研究，完成表．四边形
对称性
边
角
对角线
平行
四边形．
两组对边分别平行，两组对边分别相等．
两组对角
分别相等．对角线互相平分．
等腰
梯形轴对称图形，过平行的一组对边中点的直线是它的对称轴．
一组对边平行，另一组对边相等．
．
．
（2）演绎论证
证明等腰梯形有关角和对角线的性质．
已知：在等腰梯形ABCD中，AD∥BC，AB=DC，AC、BD是对角线．
求证：
证明：
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系．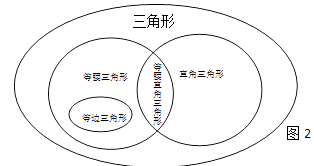
（3）请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a、b、c满足（a﹣7.5）2+
+|c﹣8.5|=0．求：（1）a、b、c的值；
（2）求以a、b、c为边构成的三角形面积．
相关试题
