【题目】如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD=![]() .
.
(1)求∠C的度数;
(2)求证:BC是⊙O的切线;
(3)求阴影部分面积.

参考答案:
【答案】(1)∠C=60°;(2)证明见解析;(3)S阴影=3π-![]() .
.
【解析】试题分析:(1)连接BD,由AD为圆的直径,得到∠ABD为直角,再利用30度角所对的直角边等于斜边的一半求出BD的长,根据CD与AB平行,得到一对内错角相等,确定出∠CDB为直角,在直角三角形BCD中,利用锐角三角函数定义求出tanC的值,即可确定出∠C的度数;
(2)连接OB,由OA=OB,利用等边对等角得到一对角相等,再由CD与AB平行,得到一对同旁内角互补,求出∠ABC度数,由∠ABC-∠ABO度数确定出∠OBC度数为90,即可得证;
(3)过O作OE⊥AB,利用30度角所对的直角边等于斜边的一半求出OE的长,根据勾股定理求出AE的长,进而求出AB的长,确定出三角形OAB面积,再由扇形AOB面积减去三角形AOB面积求出阴影部分面积即可.
试题解析:(1)如图,连接BD,
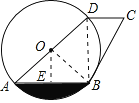
∵AD为圆O的直径,
∴∠ABD=90°,
∴BD=![]() AD=3,
AD=3,
∵CD∥AB,∠ABD=90°,
∴∠CDB=∠ABD=90°,
在Rt△CDB中,tanC=![]() =
=![]() =
=![]() ,
,
∴∠C=60°;
(2)证明:连接OB,
∵OA=OB,
∴∠OBA=∠A=30°,
∵CD∥AB,∠C=60°,
∴∠ABC=180°-∠C=120°,
∴∠OBC=∠ABC-∠ABO=120°-30°=90°,
∴OB⊥BC,
∴BC为圆O的切线;
(3)解:过点O作OE⊥AB,则有OE=![]() OA=
OA=![]() ,
,
∵AB=![]() =
=![]() =3
=3![]() ,
,
∴S△OAB=![]() ABOE=
ABOE=![]() ×3
×3![]() ×
×![]() =
=![]() ,
,
∵∠AOB=180°-2∠A=120°,
∴S扇形OAB=![]() =3π,
=3π,
则S阴影=S扇形OAB-S△AOB=3π-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形
 中,
中, ,
, ,那么
,那么 等于( )
等于( )
A. 60°B. 45°C. 30°D. 22.5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最小的正整数,且a、b满足
 .
.(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为动点,其对应的数为x,点P在-1到1之间运动时(即
 ),请化简式子:
),请化简式子: (写出化简过程);
(写出化简过程);(3)在(1)、(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒一个单位长度的速度向左运动,同时点B以每秒2个单位长度,点C以每秒5个单位长度的速度向右运动3秒钟后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请求BC-AB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )

A.
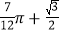 B.
B. 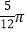 C.
C.  D.
D. 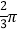
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列一元二次方程化成一般式,并写出方程中的各项及各项的系数.
(1)
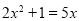 ;
;一般式:_________________.
二次项为____,二次项系数为____,一次项为____,
一次项系数为____,常数项为____.
(2)
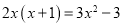 ;
;一般式:_________________.
二次项为____,二次项系数为____,一次项为____,
一次项系数为____,常数项为____.
相关试题

