【题目】已知:方程![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() 的解是x=
的解是x=![]() ,方程
,方程![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() 的解是x=
的解是x=![]() ,试猜想:
,试猜想:
(1)方程![]() +
+![]() =
=![]() +
+![]() 的解;
的解;
(2)方程![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() 的解(a、b、c、d表示不同的数).
的解(a、b、c、d表示不同的数).
参考答案:
【答案】(1)x=4;(2)x=![]() .
.
【解析】试题分析:通过解题目中已知的两个方程的过程可以归纳出方程的解与方程中的常数之间的关系,利用这个关系可得出两个方程的解.
先左右两边分别通分可得:![]() ,
,
化简可得:![]() ,
,
整理可得:2x=15﹣8,解得:x=![]() ,
,
这里的7即为(﹣3)×(﹣5)﹣(﹣2)×(﹣4),
这里的2即为[﹣2+(﹣4)]﹣[﹣3+(﹣5)];
解方程![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() ,先左右两边分别为通分可得:
,先左右两边分别为通分可得:
![]() ,化简可得:
,化简可得:![]() ,
,
解得:x=![]() ,
,
这里的11即为(﹣7)×(﹣5)﹣(﹣4)×(﹣6),
这里的2即为[﹣4+(﹣6)]﹣[﹣7+(﹣5)];
所以可总结出规律:方程解的分子为右边两个分中的常数项的积减去左边两个分母中的常数项的积,解的分母为左边两个分母中的常数项的差减去右边两个分母中常数项的差.
试题解析:(1)先把方程分为两边差的形式:方程![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() ,
,
由所总结的规律可知方程解的分子为:(﹣1)×(﹣6)﹣(﹣7)×(﹣2)=﹣8,
分母为[﹣7+(﹣2)]﹣[﹣6+(﹣1)]=﹣2,
所以方程的解为x=![]() =4;
=4;
(2)由所总结的规律可知方程解的分子为:cd﹣ab,分母为(a+b)﹣(c+d),
所以方程的解为x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:

(1)该镇本次统计的小微企业总个数是 ,扇形统计图中B类所对应扇形圆心角的度数为 度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
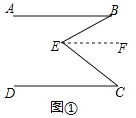
 问题发现:如图
问题发现:如图 ,直线
,直线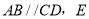 是AB与AD之间的一点,连接
是AB与AD之间的一点,连接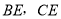 ,可以发现
,可以发现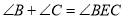 .
.

请把下面的证明过程补充完整:
证明:过点E作
 ,
, 已知
已知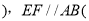 辅助线的作法
辅助线的作法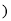 .
.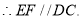 _____
_____
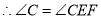 ______
______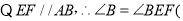 同理
同理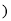 .
. _____
_____
等量代换
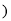
即
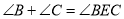 .
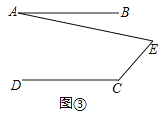
. 拓展探究:如果点E运动到图
拓展探究:如果点E运动到图 所示的位置,其他条件不变,进一步探究发现:
所示的位置,其他条件不变,进一步探究发现: 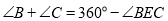 ,请说明理由.
,请说明理由.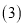 解决问题:如图
解决问题:如图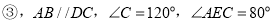 ,请直接写出
,请直接写出 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若a是(-4)2的平方根,b的一个平方根是2,求式子a+b的立方根;
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为
 ,求式子x2+(a+b+cd)x+
,求式子x2+(a+b+cd)x+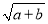 +
+ 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
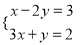 (2)
(2) 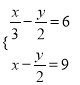
(3)
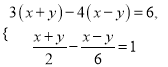 (4)
(4) 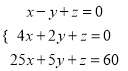
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-
 <0,求x的取值范围.
<0,求x的取值范围.
相关试题

