【题目】平面直角坐标系中,直线 ![]() 与x轴交于点A ,与y 轴交于点B,直线
与x轴交于点A ,与y 轴交于点B,直线 ![]() 与x轴交于点C,与直线
与x轴交于点C,与直线![]() 交于点P.
交于点P.
(1)当k=1 时,求点C的坐标;
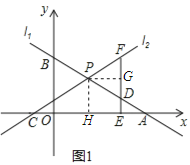
(2)如图 1,点D为PA的中点,过点D作DE⊥x轴于E,交直线![]() 于点F,若DF=2DE,求k的值;
于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ 的延长线交直线![]() 于点R,若PR=PC,求点P的坐标.
于点R,若PR=PC,求点P的坐标.


参考答案:
【答案】(1)(-2,0)(2)![]() (3)(-
(3)(-![]() ,
,![]() )
)
【解析】(1)解两个函数解析式组成的方程组即可求解;
(2)过点P作PG⊥DF于点G,易证△PDG≌△ADE,过点P作PH⊥CA于点H,可证点H是AC中点,则H的坐标即可求得,进而求得点P的坐标,再求得点K的值即可;
(3)Rt△PMC≌Rt△PQR,则RQ=MC,设NR=NC=a,则R(﹣a﹣2,a),代入y=﹣![]() x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
(1)当k=1时,直线l2为y=x+2.
解方程组 ,
,
解得![]() ,
,
∴P(![]() ,
,![]() );
);
(2)当y=0时,kx+2k=0,
∵k≠0,
∴x=﹣2,
∴C(﹣2,0)则OC=2,
当y=0时,﹣![]() x+3=0,
x+3=0,
∴x=6,
∴A(6,0),OA=6,
过点P作PG⊥DF于点G,
在△PDG和△ADE中,
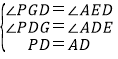 ,
,
∴△PDG≌△ADE,
得DE=DG=![]() DF,
DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH=![]() CA=4,
CA=4,
∴OH=2,
当x=2时,y=﹣![]() ×2+3=2代入y=kx+2k,得k=
×2+3=2代入y=kx+2k,得k=![]() ;
;
(3)直角△PQR和直角△PMC中,
![]() ,
,
∴Rt△PMC≌Rt△PQR,
∴CM=RQ,
∴NR=NC,
设NR=NC=a,则R(﹣a﹣2,a),
代入y=﹣![]() x+3,
x+3,
得﹣![]() (﹣a﹣2)+3=a,解得a=8,
(﹣a﹣2)+3=a,解得a=8,
设P(m,n),则 ,
,
解得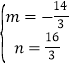 ,
,
∴P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 ,它 (填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.

①a2;②____________. ③b2 ; ④_________________.
(2)请在图④画出拼图并通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算10.232+20.46×9.77+9.772的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三点,分别表示有理数-26、-10、10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P到点A和点C的距离:PA=________,PC=_____________
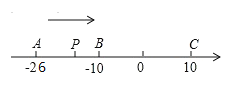
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,当点Q开始运动后,请用t的代数式表示P、Q两点间的距离。(友情提醒:注意考虑P、Q的位置)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是抛物线形拱桥,当拱顶离水面2米时,水面宽4米.若水面下降1米,则水面宽度将增加多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E.

(1)求证:AC∥DE;
(2)若OA=AE=4,求AC的长.
相关试题

