【题目】已知,AB是⊙O的直径,BC是弦,直线CD是⊙O的切线,切点为C,BD⊥CD.
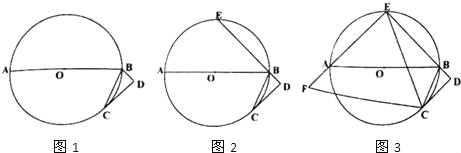
(1)如图1,求证:BC平分∠ABD;
(2)如图2,延长DB交⊙O于点E,求证:弧AC =弧EC;
(3)如图3,在(2)的条件下,连接EA并延长至F,使EF=AB,连接CF、CE,若tan∠FCE=![]() ,BC=5,求AF的长.
,BC=5,求AF的长.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)AF=EF﹣AE=![]() .
.
【解析】
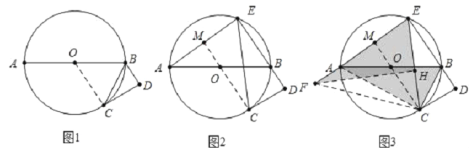
试题分析:(1)如图1中,欲证明BC平分∠ABD,只要证明∠CBD=∠CBO,只要证明BD∥OC即可.(2)如图2中,连接AE,连接CO并延长交AE于M欲证明弧AC =弧EC,只要证明CM⊥AE即可.(3)如图3中,连接AC,连接CO并延长交AE于M,过F作FH⊥CE于H,首先证明△FHE≌△ACB,根据tan∠FCE=![]() ,设FH=12k,CH=7k,列出方程求出k,通过解直角三角形分别求出EF、AE即可解决问题.
,设FH=12k,CH=7k,列出方程求出k,通过解直角三角形分别求出EF、AE即可解决问题.
试题解析:(1)证明:如图1中,连接OC,
∵AB是⊙O直径,DC是⊙O切线,
∴OC⊥CD,
∴∠OCD=90°,∵BD⊥CD,∴∠D=90°,
∴∠OCD+∠D=180°,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠OBC=∠CBD,
∴BC平分∠OBD.
(2)证明:如图2中,连接AE,连接CO并延长交AE于M.
∵AB是直径,
∴∠AEB=90°,
∵CM∥DB,
∴∠AMC=∠AEB=90°,
∴CM⊥AB,
∴∠AMC=∠AEB=90°,
∴CM⊥AB,且CM经过圆心O,
∴弧AC =弧EC.
(3)解:如图3中,连接AC,连接CO并延长交AE于M,过F作FH⊥CE于H,
∵FH⊥CE,
∴∠FHE=∠FHC=90°,
由(2)可知∠AMC=90°,
∴∠CME=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠FHE=∠ACB=90°,
∵FH=AB,∠FEH=∠ABC,
∴△FHE≌△ACB,
∴FH=AC,EH=BC,
在RT△FHC中,tan∠FCE=![]() ,设FH=12k,CH=7k,
,设FH=12k,CH=7k,
∴FH=AC=12k,
∵弧AC =弧EC,
∴CE=AC=12k,
∴EH=BC=5k,
∵BC=5,
∴5k=5,
∴k=1,∴AC=12,
在RT△ACB中,AB=![]() =13,∴AB=EF=13,
=13,∴AB=EF=13,
在RT△ACB中,sin∠ABC=![]() ,∵∠ABC=∠CBD,
,∵∠ABC=∠CBD,
在RT△CBD中,sin∠CBD=![]() ,∴CD=
,∴CD=![]() ,
,
∵∠AED=∠D=∠ACB=90°,
∴四边形CMED是矩形,
∴CD=ME=![]() ,
,
∴AM=ME,
∴AE=2ME=![]() ,
,
∴AF=EF﹣AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a﹣b|.
所以式子|x﹣2|的几何意义是数轴上表示x的点与表示2的点之间的距离.借助于数轴回答下列问题:
①数轴上表示2和5两点之间的距离是 , 数轴上表示1和﹣3的两点之间的距离是 .
②数轴上表示x和﹣2的两点之间的距离表示为 .
③数轴上表示x的点到表示1的点的距离与它到表示﹣3的点的距离之和可表示为:|x﹣1|+|x+3|.则|x﹣1|+|x+3|的最小值是 .
④若|x﹣3|+|x+1|=8,则x=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两条直线和第三条直线 , 那么这两条直线平行;若a∥b , b∥c,则 .
-
科目: 来源: 题型:
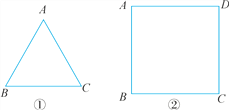
查看答案和解析>>【题目】(1)如图①,△ABC是等边三角形,△ABC所在平面上有一点P,使△PAB,△PBC,△PAC都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
(2)如图②,正方形ABCD所在的平面上有一点P,使△PAB,△PBC,△PCD,△PDA都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画以AB为斜边的等腰直角三角形ABE;
(2)在方格纸中画以CD为一边的三角形CDF,点F在小正方形的顶点上,且三角形CDF的面积为5,tan∠DCF=
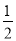 ,连接EF,并直接写出线段EF的长.
,连接EF,并直接写出线段EF的长.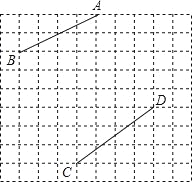
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x2-3x+n)(x2+mx+8)的结果中不含x2和x3的项,则m,n的值为( )
A. m=3,n=1 B. m=0,n=0 C. m=-3,n=-9 D. m=-3,n=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题.
(1)﹣1.3+(﹣1.7)﹣(﹣13)
(2)﹣30×( ﹣
﹣  ﹣
﹣ 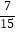 )
)
(3)(﹣2)2×3+2×(﹣32)
(4)﹣2×(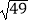 ﹣
﹣ 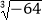 )+|﹣7|.
)+|﹣7|.
相关试题

