【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a﹣b|.
所以式子|x﹣2|的几何意义是数轴上表示x的点与表示2的点之间的距离.借助于数轴回答下列问题:
①数轴上表示2和5两点之间的距离是 , 数轴上表示1和﹣3的两点之间的距离是 .
②数轴上表示x和﹣2的两点之间的距离表示为 .
③数轴上表示x的点到表示1的点的距离与它到表示﹣3的点的距离之和可表示为:|x﹣1|+|x+3|.则|x﹣1|+|x+3|的最小值是 .
④若|x﹣3|+|x+1|=8,则x=![]()
参考答案:
【答案】3;4;x+2;4;﹣3或5
【解析】解:①数轴上表示2和5两点之间的距离是:|5﹣2|=3,
数轴上表示1和﹣3的两点之间的距离是:|1﹣(﹣3)|=4.②数轴上表示x和﹣2的两点之间的距离表示为:|x﹣(﹣2)|=|x+2|.③数轴上表示x的点到表示1的点的距离与它到表示﹣3的点的距离之和可表示为:|x﹣1|+|x+3|,
当数轴上表示x的点在表示1的点和表示﹣3的点之间时,
|x﹣1|+|x+3|的最小值是:|1﹣(﹣3)|=4.④若|x﹣3|+|x+1|=8,
Ⅰ、x≤﹣1时,
3﹣x﹣x﹣1=8,
解得x=﹣3.
Ⅱ、﹣1<x<3时,
3﹣x+x+1=8,
此时x无解.
Ⅲ、x≥3时,
x﹣3+x+1=8,
解得x=5.
所以答案是:3、4;|x+2|;4;﹣3或5.
【考点精析】通过灵活运用数轴和绝对值,掌握数轴是规定了原点、正方向、单位长度的一条直线;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】夜晚当你靠近一盏路灯时,你发现自己的影子是( )
A.变短
B.变长
C.由短变长
D.由长变短 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学张老师在课堂上提出一个问题:“通过探究知道:
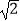 ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用 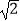 ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答: 已知8+
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答: 已知8+  =x+y,其中x是一个整数,0<y<1,求2x+(y﹣
=x+y,其中x是一个整数,0<y<1,求2x+(y﹣  )2016的值.
)2016的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的四条线段成比例的是( )
A.a=1,b=3,c=2,d=4
B.a=4,b=6,c=5,d=10
C.a=2,b=4,c=3,d=6
D.a=2,b=3,c=4,d=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两条直线和第三条直线 , 那么这两条直线平行;若a∥b , b∥c,则 .
-
科目: 来源: 题型:
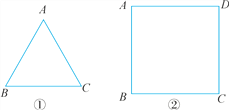
查看答案和解析>>【题目】(1)如图①,△ABC是等边三角形,△ABC所在平面上有一点P,使△PAB,△PBC,△PAC都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
(2)如图②,正方形ABCD所在的平面上有一点P,使△PAB,△PBC,△PCD,△PDA都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB是⊙O的直径,BC是弦,直线CD是⊙O的切线,切点为C,BD⊥CD.
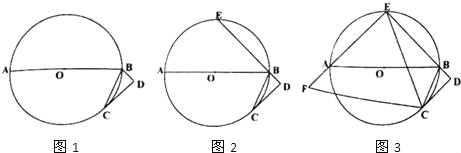
(1)如图1,求证:BC平分∠ABD;
(2)如图2,延长DB交⊙O于点E,求证:弧AC =弧EC;
(3)如图3,在(2)的条件下,连接EA并延长至F,使EF=AB,连接CF、CE,若tan∠FCE=
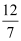 ,BC=5,求AF的长.
,BC=5,求AF的长.
相关试题

