【题目】已知一个一次函数图象经过点P(0,-3), 且经过点Q(2,3)
⑴求此一次函数表达式。
⑵求它与X轴的交点。
参考答案:
【答案】(1) y=3x-3;(2) (1,0)
【解析】试题分析:
(1)利用待定系数法即可求得函数的解析式;
(2)令y=0即可求得与x轴的横坐标.
试题解析:(1)由题意,
设此一次函数表达式为y=kx+b(k≠0),
它过点P(0,-3)把x=0,y=-3代入上式,
k×0+b=-3,得b=-3,y=kx-3,
它又过点Q(2,3),把x=2,y=3代入y=kx-3,
3=2k-3,
k=3,
所以y=3x-3.
(2)当y=0时,3x-3=0,x=1,它与x轴交于(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列式中的x的值.(2x+1)2= 9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】科学家在实验中检测出某微生物约为0.0000035米,将0.0000035用科学记数法表示为( )
A.3.5×10﹣6 B.3.5×106 C.3.5×10﹣5 D.35×10﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.
下面是一个案例,请补充完整.
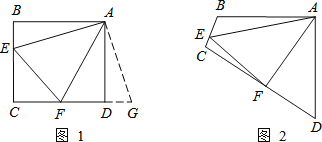
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合
∵∠ADC=∠B=90°
∴∠FDG=180°,点F、D、G共线根据SAS,易证△AFG≌ ,从而可得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF.
请写出推理过程:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<
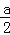 )厘米的正方形,利用因式分解计算当a=13.4,b=3.4时,剩余部分的面积.
)厘米的正方形,利用因式分解计算当a=13.4,b=3.4时,剩余部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2,+3.5,0,3,﹣0.7,11中,整数有( )
A. l个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为( )
A.7.6×10﹣9 B.7.6×10﹣8 C.7.6×109 D.7.6×108
相关试题

