【题目】如图,已知△ABC和△A″B″C″及点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若△A″B″C″与△A′B′C′关于点O′对称,请确定点O′的位置;
(3)探究线段OC′与线段CC″之间的关系,并说明理由.

参考答案:
【答案】见解析
【解析】
(1)连接三角形的各顶点与O的连线,并延长相同长度,找到对应点,顺次连接.
(2)若△A″B″C″与△A′B′C′关于点O′对称,连接两组对应点的连线的交点O就是对称点.
(1)分别作A、B、C关于O的对称点A′、B′、C′,
连接AA′,BB′,CC′,
则如图中的△A′B′C′为所求.
(2)连接A″A′,C″C′,两线交于O′,
则O′为所求.
(3)线段OC′与线段CC″之间的关系是CC″=2OC′,
理由是:∵CC′关于O对称,
∴CO=OC′,
同理C′O′=C″O′,
∵OO′为三角形CC′C″的中位线,
∴CC″=2OC′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在射线OM、ON上,当点B在ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,a)是反比例函数
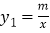 的图象上一点,直线
的图象上一点,直线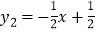 与反比例函数
与反比例函数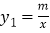 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.

(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8.求AB的长度和DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足△BCP的周长为14cm,求此时t的值;
(2)若点P在∠BAC的平分线上,求此时t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
相关试题

