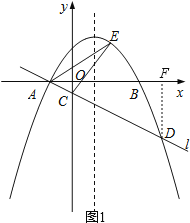
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
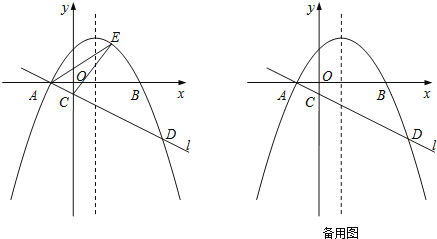
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的一点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
参考答案:
【答案】(1)y=ax+a;(2)a=﹣![]() ;(3)能,P点的坐标为P1(1,﹣4),P2(1,﹣
;(3)能,P点的坐标为P1(1,﹣4),P2(1,﹣![]() ).
).
【解析】
试题分析:(1)由抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于两点A、B,求得A点的坐标,作DF⊥x轴于F,根据平行线分线段成比例定理求得D的坐标,然后利用待定系数法法即可求得直线l的函数表达式.
(2)设点E(m,a(m+1)(m﹣3)),yAE=k1x+b1,利用待定系数法确定yAE=a(m﹣3)x+a(m﹣3),从而确定S△ACE=![]() (m+1)[a(m﹣3)﹣a]=
(m+1)[a(m﹣3)﹣a]=![]() (m﹣
(m﹣![]() )2﹣
)2﹣![]() a,根据最值确定a的值即可;
a,根据最值确定a的值即可;
(3)分以AD为对角线、以AC为边,AP为对角线、以AC为边,AQ为对角线三种情况利用矩形的性质确定点P的坐标即可.
解:(1)令y=0,则ax2﹣2ax﹣3a=0,
解得x1=﹣1,x2=3
∵点A在点B的左侧,
∴A(﹣1,0),
如图1,作DF⊥x轴于F,
∴DF∥OC,
∴![]() =
=![]() ,
,
∵CD=4AC,
∴![]() =
=![]() =4,
=4,
∵OA=1,
∴OF=4,
∴D点的横坐标为4,
代入y=ax2﹣2ax﹣3a得,y=5a,
∴D(4,5a),
把A、D坐标代入y=kx+b得![]() ,
,
解得![]() ,
,
∴直线l的函数表达式为y=ax+a.
(2)设点E(m,a(m+1)(m﹣3)),yAE=k1x+b1,
则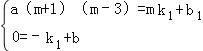 ,
,
解得: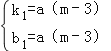 ,
,
∴yAE=a(m﹣3)x+a(m﹣3),
∴S△ACE=![]() (m+1)[a(m﹣3)﹣a]=
(m+1)[a(m﹣3)﹣a]=![]() (m﹣
(m﹣![]() )2﹣
)2﹣![]() a,
a,
∴有最大值﹣![]() a=
a=![]() ,
,
∴a=﹣![]() ;
;
(3)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,
解得x1=﹣1,x2=4,
∴D(4,5a),
∵y=ax2﹣2ax﹣3a,∴抛物线的对称轴为x=1,
设P1(1,m),
①若AD是矩形的一条边,
由AQ∥DP知xD﹣xP=xA﹣xQ,可知Q点横坐标为﹣4,将x=﹣4带入抛物线方程得Q(﹣4,21a),
m=yD+yQ=21a+5a=26a,则P(1,26a),
∵四边形ADPQ为矩形,∴∠ADP=90°,
∴AD2+PD2=AP2,
∵AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,
PD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,
∴[4﹣(﹣1)]2+(5a)2+(1﹣4)2+(26a﹣5a)2=(﹣1﹣1)2+(26a)2,
即a2=![]() ,∵a<0,∴a=﹣
,∵a<0,∴a=﹣![]() ,
,
∴P1(1,﹣![]() ).
).
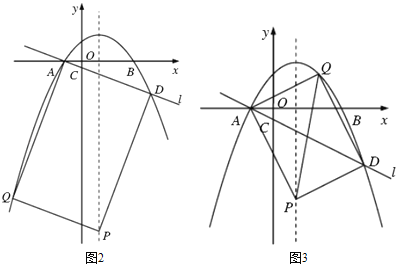
②若AD是矩形的一条对角线,
则线段AD的中点坐标为(![]() ,
,![]() ),Q(2,﹣3a),
),Q(2,﹣3a),
m=5a﹣(﹣3a)=8a,则P(1,8a),
∵四边形ADPQ为矩形,∴∠APD=90°,
∴AP2+PD2=AD2,
∵AP2=[1﹣(﹣1)]2+(8a)2=22+(8a)2,
PD2=(4﹣1)2+(8a﹣5a)2=32+(3a)2,
AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,
∴22+(8a)2+32+(3a)2=52+(5a)2,
解得a2=![]() ,∵a<0,∴a=﹣
,∵a<0,∴a=﹣![]() ,
,
∴P2(1,﹣4).
综上可得,P点的坐标为P1(1,﹣4),P2(1,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.“任意画一个三角形,其内角和为360°”是随机事件
B.已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次
C.抽样调查选取样本时,所选样本可按自己的喜好选取
D.检测某城市的空气质量,采用抽样调查法
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成图1。
探索发现:试用不同的方法计算图1的面积,你能发现a、b、c间有什么数量关系?
尝试应用:如图2,在直角三角形ABC中,∠ACB=90°,三边分别为a、b、c,
①若b-a=2,c=10,求此三角形的周长及面积。
②若b=12,a、c均为整数,试求出所有满足条件的a、c的值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距630千米,在A、B之间有汽车站C站,如图1所示.客车由A地驶向C站、货车由B地驶向A地,两车同时出发,匀速行驶,货车的速度是客车速度的
 .图2是客、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.则下列说法不正确的是( )
.图2是客、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.则下列说法不正确的是( )
A.货车行驶2小时到达C站 B.货车行驶完全程用时14小时
C.图2中的点E的坐标是(7,180) D.客车的速度是60千米∕时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果10b=n,那么称b为n的劳格数,记为b=d (n),由定义可知:10b=n与b=d (n)所表示的是b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)= ,d(10﹣2)= ;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d(
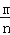 )=d(m)﹣d(n).
)=d(m)﹣d(n).根据运算性质,填空:
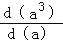 = (a为正数).
= (a为正数).(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
x
1.5
3
5
6
8
9
12
27
d(x)
3a﹣b+c
2a﹣b
a+c
1+a﹣b﹣c
3﹣3a﹣3c
4a﹣2b
3﹣b﹣2c
6a﹣3b
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校分别选派相同人数的选手参加中国成语大赛,每人成绩为A、B、C、D、E五个等级中的一种,已知两校得A等的人数相同,现将甲、乙两校比赛成绩绘制成了如图统计图,请根据图象回答问题:

(1)两校选派的学生人数分别为 名,甲校学生参加比赛获B等成绩人数在扇形统计图中的圆心角为 °;请将乙校学生得分条形统计图补充完整;
(2)甲校得E的学生中有2人是女生,乙校得E的学生中有2人是男生,现准备从这四名学生中选两名参加表演赛,请用列表或画树状图的方法求出所选的两名学生刚好是一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a是最小的正整数,b是绝对值最小的数,c与a2互为相反数,那么 (a + b)2016 c2016 = __________.
相关试题

