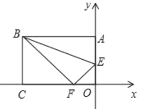
【题目】长方形纸片![]() 中,
中,![]() ,
,![]() ,把这张长方形纸片
,把这张长方形纸片![]() 如图放置在平面直角坐标系中,在边
如图放置在平面直角坐标系中,在边![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处.
处.
(1)点![]() 的坐标是____________________;点
的坐标是____________________;点![]() 的坐标是__________________________;
的坐标是__________________________;
(2)在![]() 上找一点
上找一点![]() ,使
,使![]() 最小,求点
最小,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上一个动点,设
上一个动点,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数 关系式.
的函数 关系式.
参考答案:
【答案】(1)(0,3);(﹣4,0);(2)![]() ;(3)
;(3) ![]()
【解析】
(1)根据折叠性质求出BF,再利用勾股定理求出CF,从而得出OF,在△EOF中设未知数的方法根据勾股定理列出方程求解即可.
(2)作E关于AB的对称点,连接对称点到F,利用勾股定理求出长度即可.
(3)利用待定系数法求出PF的表达式,再根据面积公式代入即可.
(1)由折叠的性质可得BF=AB=10,
∵BC=8,∠BCF=90°,
∴CF=![]() ,
,
∵OC=AB=10,
∴OF=10-6=4,即F的坐标为(﹣4,0),
设AE为x,则EF也为x,EO为8-x,
根据勾股定理得:42+(8-x)2=x2,解得x=5.
∴EO=8-5=3,即E的坐标为(0,3).
(2)作E关于AB的对称点E’,连接E’F交AB于P,此时E’F即为PE+PF最小值.

根据对称性可知AE’=AE=5,则OE’=5+8=13,
根据勾股定理可得:E’F=![]() .
.
(3)根据题意可得S=![]() .
.
设直线PF的表达式为:y=kx+13,
将点F(﹣4,0)代入,解得k=![]() ,
,
∴PF的表达式为:![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图所示,直线y1=-2x+3和直线y2=mx-1分别交y轴于点A,B,两直线交于点C(1,n).
(1)求m,n的值;
(2)求ΔABC的面积;
(3)请根据图象直接写出:当y1<y2时,自变量的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
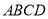 中,点
中,点 是对角线
是对角线 上一点,且
上一点,且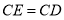 ,过点
,过点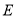 作
作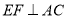 交
交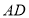 于点
于点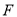 ,连接
,连接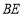 .
.(1)求证:
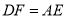 ;
;(2)当
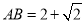 时,求
时,求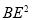 的值.
的值.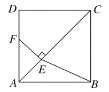
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下表:
命中环数
7
8
9
10
甲命中相应环数的次数
2
2
0
1
乙命中相应环数的次数
1
3
1
0
(1)求甲、乙两人射击成绩的平均数;
(2)甲、乙两人中,谁的射击成绩更稳定些?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
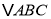 是等边三角形,延长
是等边三角形,延长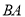 到点
到点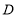 ,延长
,延长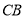 到点
到点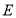 ,使
,使 ,连接
,连接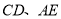 ,延长
,延长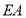 交
交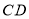 于
于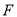 .
.(1)求证:
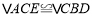 ;
;(2)求
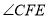 的度数.
的度数.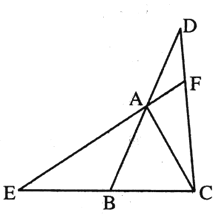
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(
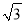 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: 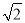 =1.41,
=1.41,  =1.73)
=1.73)
相关试题

