随着城市人口的不断增加，美化城市，答案解析
科目：czsx 来源： 题型：
科目：czsx 来源：《第22章 一元二次方程》2009年全章拔高训练题（解析版） 题型：解答题
科目：czsx 来源：不详 题型：解答题
科目：czsx 来源：数学教研室 题型：044
科目：czsx 来源： 题型：
| ( ) |
| 3 |
| ( ) |
| 5 |
| ( ) |
| 7 |
在我们的教科书中选取了一些具体值并将它们代入要解的一元二次方程中，大致估计出一元二次方程解的范围，再在这个范围内逐步加细赋值，进而逐步估计出一元二次方程的近似解．下面介绍另外一种估计一元二次方程近似解的方法，以方程x2-3x-1=0为例，因为x≠0，所以先将其变形为x=3+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 | ||
3+
|
| 1 |
| x |
| 1 | ||||||||
3+
|
可以猜想，随着替代次数的不断增加，右式最后的
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 | ||
3+
|
| 1 |
| x |
| 1 |
| 3 |
3，3+
| 1 |
| 3 |
| 1 | ||
3+
|
| 1 | ||||
3+
|
| 10 |
| 3 |
| 33 |
| 10 |
| 109 |
| 33 |
可以发现它们越来越趋于稳定，事实上，这些数越来越近似于方程x2-3x-1=0的正根，而且它的算法也很简单，就是以3为第一个近似值，然后不断地求倒数，再加3而已，在计算机技术极为发达的今天，只要编一个极为简单的程序，计算机就能很快帮你算出它的多个近似值．
科目：czsx 来源：学习周报 数学 北师大八年级版 2009－2010学年 第4期 总第160期 北师大版 题型：013
任意找一个你认为很大的正数，利用计算器对它重复进行开方运算，随着运算次数的不断增加，你发现
最终结果将接近
1最终结果将接近
0不同的数有不同的结果
以上都不对
科目：czsx 来源：《28.4 方程的近似解》2010年习题精选（解析版） 题型：解答题
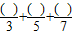≈1.16，那么你能算出他们的分子依次是哪些数吗？在我们的教科书中选取了一些具体值并将它们代入要解的一元二次方程中，大致估计出一元二次方程解的范围，再在这个范围内逐步加细赋值，进而逐步估计出一元二次方程的近似解．下面介绍另外一种估计一元二次方程近似解的方法，以方程x2-3x-1=0为例，因为x≠0，所以先将其变形为x=3+
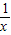，用3+
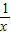代替x，得x=3+
=3+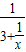
．反复若干次用3+
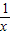代替x，就得到x=
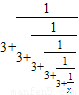形如上式右边的式子称为连分数．可以猜想，随着替代次数的不断增加，右式最后的
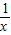对整个式子的值的影响将越来越小，因此可以根据需要，在适当时候把
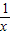忽略不计，例如，当忽略x=3+
中的
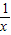时，就得到x=3；当忽略x=3+
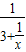中的
时，就得到x=3+
；如此等等，于是可以得到一系列分数；3，3+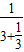
，3+
，3+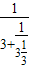
，…，即3，
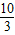=3.3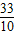33…，
≈3.3.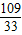
=3.303 03…，…．可以发现它们越来越趋于稳定，事实上，这些数越来越近似于方程x2-3x-1=0的正根，而且它的算法也很简单，就是以3为第一个近似值，然后不断地求倒数，再加3而已，在计算机技术极为发达的今天，只要编一个极为简单的程序，计算机就能很快帮你算出它的多个近似值．
科目：czsx 来源： 题型：单选题
任意找一个你认为很大的正数，利用计算器对它重复进行开方运算，随着运算次数的不断增加，你发现
- A.最终结果将接近1
- B.最终结果将接近0
- C.不同的数有不同的结果
- D.以上都不对
科目：czsx 来源： 题型：阅读理解
| x（元） | 0 | 100 | 200 | 300 | … |
| y（亩） | 800 | 1600 | 2400 | 3200 | … |
| z（元） | 3000 | 2700 | 2400 | 2100 | … |
（2）要使该地区种植树苗的总收益w（元）最大，政府应将每亩补贴数额x定为多少？并求出总收益w的最大值和此时种植的亩数；（总收益=种植亩数×每亩树苗的收益）
（3）在取得最大收益的情况下，经市场调查，培育种植水果类树苗经济效益更好．今年该地区决定用种植树苗总面积m%的土地种植水果类树苗，因环境和经济等因素的制约，种植水果类树苗的面积不超过300亩．经测算，种植水果类树苗需用的支架、塑料膜等材料每亩费用为2700元，此外还需购置喷灌设备，这项费用（元）与种植水果类树苗面积（亩）的平方成正比例，比例系数9．预计今年种植水果类树苗后的这部分土地的收益比没种前的收益每亩增加了7500元，这样，该地区今年因种植水果类树苗而增加的收益（扣除材料费和设备费后）共570000元，求m的值．（结果精确到个位，参考数据：
| 7 |
| 11 |
科目：czsx 来源： 题型：
（1）求2006年底至2008年底我市汽车拥有量的年平均增长率；
（2）为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）
科目：czsx 来源： 题型：
| x（元） | 0 | 100 | 200 | 300 | … |
| y（亩） | 800 | 1600 | 2400 | 3200 | … |
| z（元） | 3000 | 2700 | 2400 | 2100 | … |
（2）要使全县这种蔬菜的总收益w（元）最大，政府应将每亩补贴数额x定为多少并求出总收益w的最大值和此时种植亩数；
（3）在取得最大收益的情况下，为了满足市场需求，用不超过70亩的土地对这种蔬菜进行反季节的种植．为此需修建一些蔬菜大棚，修建大棚要用的支架、塑料膜等材料平均每亩的费用为650元，此外还要购置喷灌设备，这项费用（元）与大棚面积（亩）的平方成正比例，比例系数为25．这样，修建大棚后的这部分土地每亩的平均收益比没修前增加了2000元，在扣除修建费后总共增加了85000元．求修建了多少亩蔬菜大棚．（结果精确到个位，参考数据：
| 2 |
科目：czsx 来源： 题型：
（1）
（2）用一句话概括世界人口的变化趋势：
科目：czsx 来源： 题型：
的收益z（元）会相应降低，且z与x之间也大致满足z=-3x+3000（1）求出政府补贴政策实施后，种植亩数y与政府补贴数额x 之间的函数关系式；
（2）在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？
（3）要使全市这种蔬菜的总收益W（元）最大，政府应将每亩补贴数额X定为多少？并求出总收益W的最大值．
（4）该市希望这种蔬菜的总收益不低于7200 000元，请你在坐标系中画出3种的函数图象的草图，利用函数图象帮助该市确定每亩补贴数额的范围，在此条件下要使总收益最大，说明每亩补贴数额应定为多少元合适？
科目：czsx 来源： 题型：
| x（元） | 0 | 100 | 200 | 300 | … |
| y（亩） | 400 | 600 | 800 | 1000 | … |
| z（元） | 2400 | 2100 | 1800 | 1500 | … |
（2）政府出台补贴措施后，要使该地这种蔬菜的总收益w（元）最大，政府应该将每亩补贴数额x定为多少元？并求出总收益w的最大值和此时种植亩数．
（3）若该地今年刚好取得最大总收益，为提高菜农的经济收入，农业部门通过对种子的技术改良，每亩收益将逐步提高，计划每年一亩今年、明年、后年三年共收益5460元，求明年、后年平均每年提高的百分率．
科目：czsx 来源： 题型：
（1）设购买A型旅游车x辆，购车总费用为y万元，载客总量增加z人，分别求出y与x、z与x之间的函数关系式．
（2）若该旅行社计划购车资金为370万元至430万元之间，那么共有几种购车方案？
（3）在上面的几种购车方案中，选择哪一种购车方案可使载客量最大？最大载客量是多少？
科目：czsx 来源： 题型：阅读理解
| x（元） | 0 | 100 | 200 | 300 | 400 |
| y（亩） | 600 | 1000 | 1400 | 1800 | 2200 |
（1）请观察题中的表格，用学过的一次函数、反比例函数或二次函数的有关知识求出育苗亩数y（亩）与政府每亩补贴数额x（元）之间的函数关系式；
（2）当2010年政府补贴每亩数额x（元）是多少元时，该地区苗圃的收益w（元）最大，最大收益是多少？
（3）在2010年苗圃取得最大收益的育苗情况下，该地区培植面积刚好达到最大化，要想增收，只能提高每亩收益．经市场调查，培育银杏树苗畅销，每亩的经济效益相应会更好．2011年该地区用去年培育面积的（30-a）%的土地培育银杏树苗，其余面积继续培育一般类树苗，预计今年培育银杏树苗每亩收益在去年培育一般类树苗每亩收益的基础上增加了（100+3a）%，由于培育银杏树苗每亩多支出1000元，2011年该地区因培育银杏类树苗预计比去年增收399万元．请参考以下数据，通过计算，估算出a的整数值．（参考数据：
| 35 |
| 37 |
| 39 |
科目：czsx 来源： 题型：
| x（元） | 0 | 100 | 200 | 300 | … |
| y（亩） | 800 | 1600 | 2400 | 3200 | … |
| z（元） | 3000 | 2700 | 2400 | 2100 | … |
（2）要使全县这种蔬菜的总收益w（元）最大，政府应将每亩补贴数额x定为多少？并求出总收益w的最大值和此时种植亩数．
（3）在取得最大收益的情况下，为了满足市场需求，用不超过70亩的土地对这种蔬菜进行反季节的种植．为此需修建一些蔬菜大棚，修建大棚要用的支架、塑料膜等材料平均每亩的为650元，此外还要购置喷灌设备，这项费用（元）与大棚面积（亩）的平方成正比例，比例系数为25．这样，修建大棚后的这部分土地每亩的平均收益比没修前增加了2000元，在扣除修建费后总共增加了85000元．求修建了多少亩蔬菜大棚？（结果精确到个位，参考数据：
| 2 |
科目：czsx 来源： 题型：阅读理解
重庆市垫江县具有2000多年的牡丹种植历史．每年3月下旬至4月上旬，主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放，美不胜收．由于牡丹之根———丹皮是重要中药材，目前已种植有60多个品种2万余亩牡丹的垫江，因此成为我国丹皮出口基地，获得“丹皮之乡”的美誉。为了提高农户收入，该县决定在现有基础上开荒种植牡丹并实行政府补贴，规定每新种植一亩牡丹一次性补贴农户若干元，经调查，种植亩数
(亩)与补贴数额
(元)之间成一次函数关系，且补贴与种植情况如下表：
| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
随着补贴数额的不断增大，种植规模也不断增加，但每亩牡丹的收益
(元)会相应降低，且该县补贴政策实施前每亩牡丹的收益为3000元，而每补贴10元(补贴数为10元的整数倍)，每亩牡丹的收益会相应减少30元．
(1)分别求出政府补贴政策实施后，种植亩数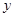(亩)、每亩牡丹的收益(元)与政府补贴数额(元)之间的函数关系式；
(2)要使全县新种植的牡丹总收益
(元)最大，又要从政府的角度出发，政府应将每亩补贴数额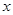定为多少元？并求出总收益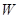的最大值和此时种植亩数；(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下，为了发展旅游业，需占用其中不超过50亩的新种牡丹园，利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”．已知引进该新品种平均每亩的费用为530元，此外还要购置其它设备，这项费用(元)等于种植面积(亩)的平方的25倍．这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元，这部分混种土地在扣除所有费用后总收益为85000元．求混种牡丹的土地有多少亩？(结果精确到个位)(参考数据：
)