扫码下载APP
返回顶部
精英家教网 > 试题搜索列表 >搜索试题

搜索试题答案解析

科目：czsx 来源： 题型：

李阳同学在“百度”搜索引擎中输入“魅力从化”，能搜索到与之相关的结果个数约为59 300，这个数用科学记数法表示为（　　）

查看答案和解析>>

科目：czsx 来源： 题型：

10、在“百度”搜索引擎中输入“姚明”，能搜索到与之相关的网页约27000000个，将这个数用科学记数法表示为
2.7×107
．

查看答案和解析>>

科目：czsx 来源： 题型：

有一道试题：“先化简，再求值：(
x-3
x+3
+
6x
x2-9
)÷
1
x2-9
，其中“x=-
2009
”．小亮同学在做题时把“x=-
2009
”错看成了“x=
2009
”，但他的计算结果确也是正确，请你说明这是什么原因？

查看答案和解析>>

科目：czsx 来源： 题型：阅读理解

阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：
问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知
13x+5y+9z=9.25---(1)
2x+4y+3z=3.20----(2)
；
视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．
解法1：视x为常数，依题意得
5y+9z=9.25-13x---(3)
4y+3z=3.20-2x----(4)
．
解这个关于y、z的二元一次方程组得
y=0.05+x
z=1-2x
．
于是x+y+z=x+0.05+x+1-2x=1.05．
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组，解答方法同上，你不妨试试．
分析：视x+y+z为整体，由（1）、（2）恒等变形得5（x+y+z）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20．
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方
程组
5a+4b=9.25---(5)
4a-b=3.20----(6)
．
由⑤+4×⑥，得21a+22.05，a=1.05．
评注：运用整体的思想方法指导解题．视x+y+z，2x+z为整体，令a=x+y+z，b=2x+z，代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解．
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
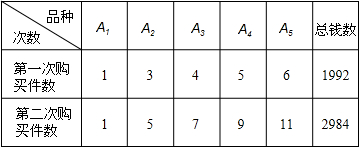
精英家教网
那么，购买每种教学用具各一件共需多少元？

查看答案和解析>>

科目：czsx 来源： 题型：

明天数学课要学“二次函数”，小明在“百度”搜索引擎中输入“二次函数”，能搜索到与之相关的结果个数约为7570000，这个数用科学记数法表示为（　　）

查看答案和解析>>

科目：czsx 来源： 题型：

钓鱼岛是我国的固有领土．近段时间，中日钓鱼岛事件成了各大新闻网站的热门话题．某天，肖璇在“百度”搜索引擎中输入“钓鱼岛事件最近进展”，能搜索到相关结果约805000个，把805000用科学记数法表示为（　　）

查看答案和解析>>

科目：czsx 来源： 题型：

12、百度搜索网站举行“2010年央视春节联欢晚会，你最喜欢什么节目”网上投票活动．小明同学想根据条形图中的信息再绘张扇形统计图，请问刘谦的魔术在扇形统计图中所占的圆心角为（　　）

查看答案和解析>>

科目：czsx 来源： 题型：

已知：正方形的边长为1
（1）如图①，可以算出正方形的对角线为
 
，求两个正方形并排拼成的矩形的对角线长，n个呢
？
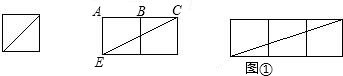
精英家教网
（2）根据图②，求证△BCE∽△BED；
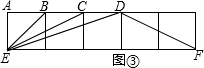
精英家教网精英家教网
（3）由图③，在下列所给的三个结论中，通过合情推理选出一个正确的结论加以证明，1．∠BEC+∠BDE=45°；⒉∠BEC+∠BED=45°；⒊∠BEC+∠DFE=45°
注意：你完成整张试卷全部试题的解答后，如果还有时间在图③中发现新的结论（不准添加辅助线和其它字母）并加以证明，将酌情加1～3分．

查看答案和解析>>

科目：czsx 来源： 题型：

七年级进行数学竞赛，初赛试题共20道题，每题答对得10分，错答或不答都扣5分，若得分超过90分可进入复赛，则进入复赛的每位同学至少得答对（　　）
A、12道题
B、12
1
3
道题
C、12
2
3
道题
D、13道题

查看答案和解析>>

科目：czsx 来源： 题型：

21、我区部分学生参加了某年全市初中数学竞赛初赛，并取得优异成绩．已知竞赛成绩分数都是整数，试题满分为120分，参赛学生的成绩分数分布情况如下：
分数段 0～19 20～39 40～59 60～79 80～99 100～119
人数 0 22 38 81 47 12
请根据以上信息解答下列问题：
（1）全区共有多少学生参加了这次全市初中数学竞赛初赛？最低分和最高分分别在什么分数范围？
（2）经竞赛组委会评定，竞赛成绩在80分以上的考生均可参加全市初中数学竞赛决赛，问：我区参加这次竞赛决赛的考生数是初赛考生数的百分之几？
（3）初赛成绩分数的中位数落在哪个分数段内？
（4）上表还提供了其他信息，例如：“没有参加决赛的的人数为141人”等等，请你再写出一条此表所提供的信息．

查看答案和解析>>

科目：czsx 来源： 题型：

加试题
（1）已知a+a-1=3，则
a2
a4-a2+1
=
1
6
=
1
6
．
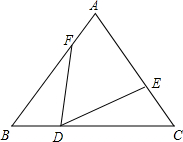
（2）如图，在△ABC中，AB=AC，D、E、F分别在BC、AC、AB上，BD=CE，CD=BF，则∠EDF=
90°-
1
2
∠A
90°-
1
2
∠A

A、90°-
1
2
∠A     B、90°-∠A     C、180°-∠A     D、180°-2∠A
（3）安岳A地有柠檬100吨，B地有柠檬80吨，计划送往甲、乙两厂深加工，甲厂需要柠檬110吨，乙厂需要柠檬70吨，从A、B两地到甲、乙两厂的路程和运费如下表：
路程（千米） 运费（元/吨．千米）
A地 B地 A地   B地
甲厂  20  15  12    12
乙厂  25  20  10    8
①若A地运往甲厂柠檬x吨，请写出将所有柠檬运往甲、乙两厂的总运费y（元）与x吨的函数关系式；
②当A、B两地运往甲、乙两厂多少吨柠檬时，总运费最少？最少运费是多少？

查看答案和解析>>

科目：czsx 来源： 题型：

某中学九年级部分同学参加全国初中数学竞赛，指导老师统计了所有参赛同学的成绩（成绩都是整数，试题满分120分），并且绘制了频数分布直方图，如图所示，请根据直方图回答下列问题：
（1）该中学参加本次数学竞赛的有多少名同学？
（2）如果成绩在90分以上（含90分）的同学获奖，那么该中学参赛同学的获奖率是多少？
（3）图中还提供了其他数据，例如该中学没有获得满分的同学等等．请再写出两条信息．

查看答案和解析>>

科目：czsx 来源： 题型：

（2011•海安县模拟）如图，我海域A港口的雷达站接到东北方向C处渔船的遇险求助后，立即命令在北偏东75°方向的B处执勤的渔政船前往救援，接到命令后，渔政船搜索到渔船C在其北偏西60°方向上，且相距120海里，并立即派出直升机施救．问接到命令时渔政船到A港口的距离是多少海里？（结果保留根号）

查看答案和解析>>

科目：czsx 来源： 题型：

（2013•常德）打开百度搜索栏，输入“数学学习法”，百度为你找到的相关信息有12000000条，请用科学记数法表示12000000=
1.2×107
1.2×107
．

查看答案和解析>>

科目：czsx 来源： 题型：

2、在“百度”搜索引擎中输入“姚明”，能搜索到与之相关的网页约27000000个，将这个数用科学记数法表示为（　　）

查看答案和解析>>

科目：czsx 来源： 题型：

一张试卷共25道题，做对一道题得4分，做错一道题扣1分．小明做了全部试题，若得分超过70分，那么小明至少做对的题数是（　　）

查看答案和解析>>

科目：czsx 来源： 题型：

在一次“人与自然”知识竞赛中，竞赛试题共有25道题，每道题都给出4个答案，其中只有一个答案正确，要求学生把正确答案选出来，每道题选对得4分，不选或选错倒扣2分，如果一个学生在本次竞赛中的得分不低于60分，那么他至少选对几道题？

查看答案和解析>>

科目：czsx 来源： 题型：

2008河南中招试题中第16题是这样的“先化简再求值：
1
a-1
-
a
a2-2a+1
÷
1
a
，其中a=1-
2
”．认真审一下题，你会发现，中招试题不过如此，只要细心，易如反掌，试试解答一下．

查看答案和解析>>

科目：czsx 来源： 题型：

对于试题：“先化简，再求值：
x-3
x2-1
-
1
1-x
，其x=2”某同学写出了如下解答：
她的解答正确吗？如不正确，请你写出正确解答．
解：
x-3
x2-1
-
1
1-x
=
x-3
(x+1)(x-1)
-
1
x-1

=
x-3
(x+1)(x-1)
-
x+1
(x+1)(x-1)

=x-3-（x+1）
=x-3+x+1
=2x-2；
当x=2时，原式=2×2-2=2．

查看答案和解析>>

科目：czsx 来源： 题型：

在“百度”搜索引擎中输入“南安”，能搜索到与之相关的网页约24 600 000个，将这个数字用科学记数法表示为（　　）

查看答案和解析>>