 加试题
加试题(1)已知a+a-1=3,则
| a2 |
| a4-a2+1 |
=
| 1 |
| 6 |
=
.| 1 |
| 6 |
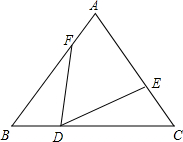
(2)如图,在△ABC中,AB=AC,D、E、F分别在BC、AC、AB上,BD=CE,CD=BF,则∠EDF=
90°-
∠A
| 1 |
| 2 |
90°-
∠A
| 1 |
| 2 |
A、90°-
| 1 |
| 2 |
(3)安岳A地有柠檬100吨,B地有柠檬80吨,计划送往甲、乙两厂深加工,甲厂需要柠檬110吨,乙厂需要柠檬70吨,从A、B两地到甲、乙两厂的路程和运费如下表:
| 路程(千米) | 运费(元/吨.千米) | |||
| A地 | B地 | A地 | B地 | |
| 甲厂 | 20 | 15 | 12 | 12 |
| 乙厂 | 25 | 20 | 10 | 8 |
②当A、B两地运往甲、乙两厂多少吨柠檬时,总运费最少?最少运费是多少?
分析:(1)先将条件变形为a+
=3,可以得到a2+
=7,根据求倒数的方法可以求出结论;
(2)根据等腰三角形的性质可以得出∠B=∠C,再证明△BDE≌△CED,根据全等三角形的性质及等腰三角形的性质可以求出结论;
(3)①设A地运往甲厂柠檬x吨,则A地运往乙厂(100-x)吨,B地运往甲厂(110-x)吨,B地运往乙厂(x-30)吨,根据总运费等于各部分运费之和就可以求出解析式;
②根据①的解析式的性质和自变量的取值范围可以求出y的最小值.
| 1 |
| a |
| 1 |
| a2 |
(2)根据等腰三角形的性质可以得出∠B=∠C,再证明△BDE≌△CED,根据全等三角形的性质及等腰三角形的性质可以求出结论;
(3)①设A地运往甲厂柠檬x吨,则A地运往乙厂(100-x)吨,B地运往甲厂(110-x)吨,B地运往乙厂(x-30)吨,根据总运费等于各部分运费之和就可以求出解析式;
②根据①的解析式的性质和自变量的取值范围可以求出y的最小值.
解答:解:(1)∵a+a-1=3,
∴a2+
=7.
∵
的倒数为:a2+
-1,
∴a2+
-1=7-1=6,
∴原式的值为:
.
故答案为:
;
(2)∵AB=AC,
∴∠B=∠C.
在△△BDE和△CED中,
,
∴△BDE≌△CED(SAS),
∴∠BFD=∠CDE.
∵∠FDC=∠B+∠BFD,
∴∠FDC-∠EDC=∠B,
即∠FDE=∠B,
∵∠B+∠C=180°-∠A,
∴∠B=90°-
∠A.
∠FDE=90°-
∠A.
故答案为:90°-
∠A.
(3)①设A地运往甲厂柠檬x吨,则A地运往乙厂(100-x)吨,B地运往甲厂(110-x)吨,B地运往乙厂(x-30)吨,由题意得:
y=20×12x+10×25(100-x)+12×15(110-x)+20×8(x-30),
y=-30x+40000,
②由题意,得
,
解得:30≤x≤100.
∵y=-30x+40000,
∴k=-30<0,
∴y随x的增大而减小,
∴当x=100时,y最小=28000.
∴设A地运往甲厂柠檬100吨,则A地运往乙厂0吨,B地运往甲厂10吨,B地运往乙厂70吨.其运费最少为28000元.

∴a2+
| 1 |
| a2 |
∵
| a2 |
| a4-a2+1 |
| 1 |
| a2 |
∴a2+
| 1 |
| a2 |
∴原式的值为:
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
(2)∵AB=AC,
∴∠B=∠C.
在△△BDE和△CED中,
|
∴△BDE≌△CED(SAS),
∴∠BFD=∠CDE.
∵∠FDC=∠B+∠BFD,
∴∠FDC-∠EDC=∠B,
即∠FDE=∠B,
∵∠B+∠C=180°-∠A,
∴∠B=90°-
| 1 |
| 2 |
∠FDE=90°-
| 1 |
| 2 |
故答案为:90°-
| 1 |
| 2 |
(3)①设A地运往甲厂柠檬x吨,则A地运往乙厂(100-x)吨,B地运往甲厂(110-x)吨,B地运往乙厂(x-30)吨,由题意得:
y=20×12x+10×25(100-x)+12×15(110-x)+20×8(x-30),
y=-30x+40000,
②由题意,得
|
解得:30≤x≤100.
∵y=-30x+40000,
∴k=-30<0,
∴y随x的增大而减小,
∴当x=100时,y最小=28000.
∴设A地运往甲厂柠檬100吨,则A地运往乙厂0吨,B地运往甲厂10吨,B地运往乙厂70吨.其运费最少为28000元.
点评:本题考查了一次函数的运用,分式的化简求值的运用,全等三角形的判定与性质的运用,等腰三角形的性质的运用.

