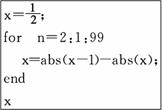1.下列对一组数据的分析,不正确的说法是( )
A.数据极差越小,样本数据分布越集中、稳定
B.数据平均数越小,样本数据分布越集中、稳定
C.数据标准差越小,样本数据分布越集中、稳定
D.数据方差越小,样本数据分布越集中、稳定
2.设m=10,n=20,则可以实现m、n的值互换的程序是( )
A.m=10 n=20 n=m m=n
B.m=10 n=20 s=m n=s
C.m=10 n=20 s=m m=n n=s
D.m=10 n=20 s=m t=s n=s m=n
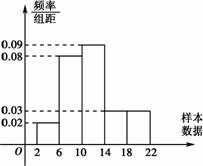
3.下图是容量为200的样本的频率分布直方图,那么样本数据落在[10,14)内的频率、频数分别为( )
C.0.36;64 D.0.36;72
4.某人在打靶中,连续射击2次,事件“至少有一次中靶”的互斥事件是( )
A.至多有一次中靶 B.两次都中靶
C.两次都不中靶 D.只有一次中靶
5.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2).则完成(1)、(2)这两项调查宜采用的抽样方法依次是( )
A.分层抽样法,简单随机抽样法
B.分层抽样法,系统抽样法
C.系统抽样法,分层抽样法
D.简单随机抽样法,分层抽样法
6.在Scilab界面内,输入如下程序:
-->j=1;
-->while j*j<1 000,j=j+1;end
-->j=j-1;
-->j
在输入完程序,击Enter键后,输出的j值为( )
A.29
B
7.先后抛掷两颗骰子,设出现的点数之和分别是12,11,10的概率依次是P1,P2,P3,则( )
A.P1=P2<P3 B.P1<P2<P3
C.P1<P2=P3 D.P3=P2<P1
8.若过直角三角形ABC的直角顶点A任作一条直线l,则l与斜边BC相交的概率为( )
A. B. C. D.
9.下面程序框图所表示的算法的功能是( )
A.计算1+++…+的值
B.计算1+++…+的值
C.计算1+++…+的值
D.计算1+++…+的值
10.以下给出的是计算1+++…+的值的一个程序框图,其中判断框内应填入的条件是( )
A.k≤10 B.k<10
C.k≤19 D.k<19
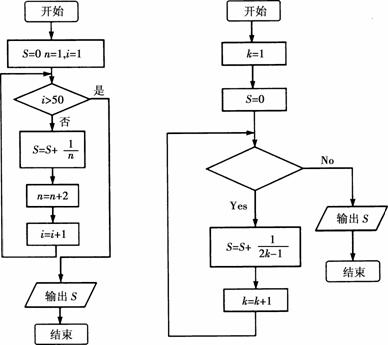
第9题图 第10题图
11.为了在运行下列程序之后输出y=9,键盘输入的x值应为 .
x=input(“x=”);
if x<0
y=(x+1)*(x+1);
else
y=x-4;
end
print(%io(2),y);
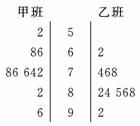
12.某中学高二年级从甲乙两个班中各随机抽取10名学生,依据他们的数学成绩画出如图所示的茎叶图,则甲班10名学生数学成绩的中位数是 ,乙班10名学生数学成绩的中位数是 .
13.假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标.现从850袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时,先将850袋牛奶按001,002,…,850进行编号.如果从随机数表第3行第1组数开始向右读,最先读到的4袋牛奶的编号是614,593,379,242,请你以此方式继续向右读数,随后读出的4袋牛奶的编号是 , , , .(下面摘取了随机数表第1行至第5行)
78 226 85 384 40 527 48 987 60 602 16 085 29 971 61 279
43 021 92 980 27 768 26 916 27 783 84 572 78 483 39 820
61 459 39 073 79 242 20 372 21 048 87 088 34 600 74 636
63 171 58 247 12 907 50 303 28 814 40 422 97 895 61 421
42 372 53 183 51 546 90 385 12 120 64 042 51 320 22 983
14.某射箭运动员一次射箭击中10环、9环、8环的概率分别是0.2、0.3、0.3,那么他射箭一次小于8环的概率是 .
15.经过市场调查分析得知,2008年第一季度内,北京市海淀区居民对某种商品的需求量为18 000件.为保证商品不脱销,商家在月初时将商品按相同数量投放市场.已知年初商品的库存量50 000件,用K表示商品的库存量,请设计一个程序框图,求出第一季度结束时商品的库存量.
17.一只口袋内装有大小相同的5只球,其中3只白球,2只黑球.现从口袋中每次任取一球,每次取出不放回,连续取两次.问:
(1)取出的两只球都是白球的概率是多少?
(2)取出的两只球中至少有一个白球的概率是多少?
卷二(共30分)
1.下面程序输出的结果是 .(注:abs(x)表示x的绝对值)
2.已知x是[-10,10]上的一个随机数,则使x满足x2-x-6≤0的概率为 .
3.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量p=(m,n),
q=(2,6),则向量p与q共线的概率为 .
4.一企业生产不同型号的水泥19 500袋,它们来自甲、乙、丙3条不同的生产线,为检查这些水泥的质量,决定采用分层抽样的方法进行检测.已知甲、乙、丙三条生产线抽取的个体数组成一个等差数列,则乙生产线生产了
袋水泥.
5.有5张卡片,上面分别标有数字0,1,2,3,4.求:
①从中任取二张卡片,二张卡片上的数字之和等于4的概率;
②从中任取2次卡片,每次取1张,第一次取出卡片,记下数字后放回,再取第二次.两次取出的卡片上的数字之和恰好等于4的概率.
6.下图是一个程序框图,其中判断框①处缺少一个判断条件,②为一输出框.
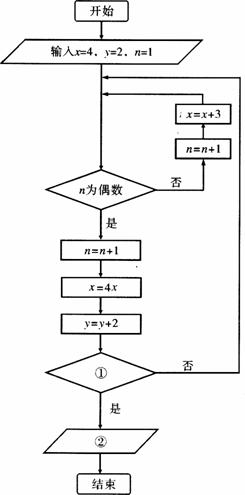
(Ⅰ)若在①处填空“n=
(Ⅱ)若在①处填空“x>22008-